
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
تحليل فوريير لشكل الخطوط: Fourier Analysis of Line profiles
المؤلف:
أ.د. نعيمة عبد القادر أحمد / أ.د. محمد أمين سلمان
المصدر:
علم البلورات والاشعة السينية
الجزء والصفحة:
ص342–343
2023-10-07
1511
أفضل طريقة لإجراء تصحيح لعرض الخطوط نتيجة الظروف العملية هي طريقة التحليل الالتفافي Convolution analysis وتبعا لهذه النظرية فإن لأي جهاز للحيود دالة (ε) g حيث يمكن تحويل الشكل النقي لخطوط الحيود (ε) f إلى الشكل (ε) h المشاهد عمليا حسب المعادلة:

في البدايات تمكن جونز Jones من إثبات أن مثل هذه المعادلة تعطي العلاقة بين شكل الخط النقي pure diffraction maximum وشكل الخط الذي نحصل عليه عمليا، ثم أوضح كل من Paterson, stokes, shall كيف أن الدالة (ε) f يمكن الحصول عليها من الدوال المقاسة عمليا (ε) g، (ε) h باستخدام نظرية تحويلات فوريير Fourier transform كالآتي:
نفترض أن الدوال (ε) g، (ε) h، (ε) f يمكن تمثيلها بمتسلسلة فوريير:
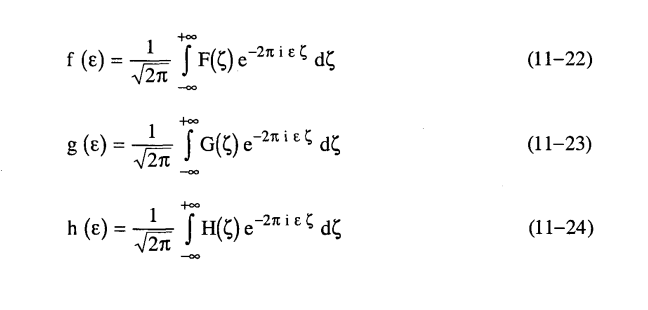
في هذه المعادلات تكون المعاملات H، G، F هي تحويلات فوريير Fourier transforms للمتغيرات h، g، f ويمكن أن تعطى بمعادلات كالمعادلة الآتية:

وبالتعويض عن h، g، f من المعادلات (22-11), (23-11), (24-11) في (20-11) نحصل على ...
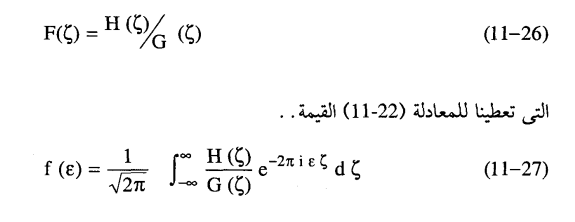
وهذا التكامل يجعل من الممكن حساب شكل الحيود النقي f من معرفة تحويل فوريير لكل من الدوال المقاسة h، g، ويمكن استبدال شكل التكامل في المعادلة بالشكل الأسي حيث يكون أكثر عمومية للسماح له بأن يجري التكامل على الدوال المتماثلة وغير المتماثلة.
وتبعا لطريقة ستوكس Stoke's method يتم استبدال التكامل بالتجميع كما تغير حدود ε من ∞ ± إلى εm ± وهي النهاية الصغرى للمتغير ε حيث يحدث للقيم الأبعد فيها أن تقل شدة الأشعة إلى قيمة شدة الخلفية back ground وعلى هذا يمكن كتابة (27-11) كالآتي:
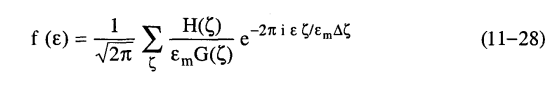
 الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
الاكثر قراءة في مواضيع عامة في الفيزياء الصلبة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















