مع أن المعلومات المحتواة في نتائج اختزال بيانات الحيود لا يمكن استخدامها بصفة مباشرة في تعيين التركيب البلوري إلا أنه يمكن الحصول منها على حقائق مفيدة فمن المقارنة بين البيانات العملية وتلك المتوقعة نظريا لبلورة تتكون من ترتيب عشوائي للذرات يمكن وضع قيم F في المقياس المطلق كذلك يمكن الحصول على معامل الذبذبة الحراري للذرات وتسمى هذه الطريقة طريقة ويلسون  Wilson.A. J. C

وكمقدمة لهذه الطريقة يجب أن نأخذ في الاعتبار تأثير درجة الحرارة على شدة الأشعة المنعكسة فكما أوردنا سابقا فإن انخفاض قدرة الذرة على التشتيت للانعكاسات التي تزيد فيها قيمة λ/θsin يعزى إلى حجم السحابة الإلكترونية المحدودة حول النواة. وكلما ازدادت هذه السحابة لعدد معين من الإلكترونات ازدادت سرعة النقصان في معامل الاستطارة (التشتت). والشكل البياني الطبيعي لمعامل الاستطارة يمكن حسابه على أساس التوزيع الإلكتروني في الذرة الساكنة ولكن في الواقع تكون الذرات في البلورات دائما متذبذبة حول أماكنها الساكنة ومقدار التذبذب يعتمد على درجة الحرارة وكتلة الذرة وكذلك على القوى التي تجعلها ثابتة في مكانها بواسطة رابطة تساهمية مثلا أو غيرها وبصفة عامة كلما ازدادت الحرارة ازدادت الذبذبة.

ويكون تأثير الحركة الحرارية هذه هو انتشار الكثافة الإلكترونية على حجم أكبر، وهذا يجعل قدرة الذرة على الاستطارة تقل بسرعة أكثر منها في حالة الذرة المثالية في التركيب الساكن، وقد أمكن نظريا وعمليا إثبات أن القدرة على الاستطارة تتغير حسب المعادلة:

حيث تكون العلاقة بين B ومتوسط السعة المربعة (μ̅ ²) للذبذبة الذرية كالاتي:

أي أن معامل الاستطارة لذرة حقيقية ليس ببساطة f₀ ولكنه عبارة عن:

انظر شكل (7-3).

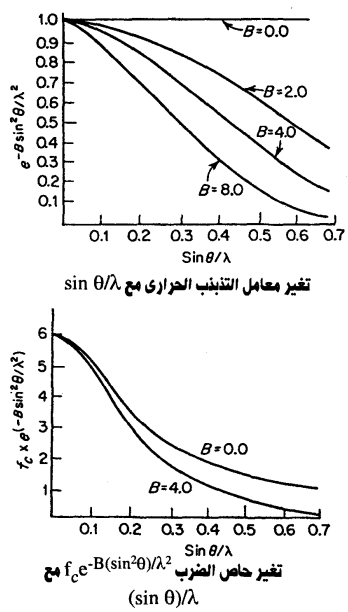
(3-7)

ومن الأفضل الحصول على قيمة B للبلورة كلها قبل بداية تعيين التركيب، ومع أن التجارب أثبتت أنه يمكن التكهن بقيمة عادة تكون ما بين 2.0 إلى 5.0 Å إلا أن طريقة ويلسون تعطينا قيمة أدق.

والآن دعنا نعرف قيمة لمتوسط شدة الانعكاس التي صوبت لمعاملي لورنتز والاستقطاب L_P بحيث تكون كالآتي:

وفي حالة الوحدة البنائية التي تحتوي على عدد N من الذرات يمكن إثبات أن متوسط شدة الانعكاس نظريا يعطى بالمعادلة:

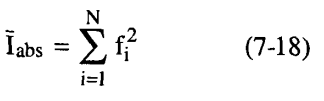
أي أن متوسط شدة الأشعة يعتمد على ما هو موجود في الوحدة البنائية للبلورة وليس على مكان وجودها، وحيث إن المشكلة هي مشكلة إحصائية فلذلك نشأت صعوبات إن كانت محتويات الوحدة تختلف كثيرا عن التوزيع العشوائي ولكن في حالة المركبات العضوية فالحال ليس كذلك والنسبة بين ̅I_abs̅ و I_rel̅ يجب أن تكون هي مقدار معامل القياس scaling factor المطلوب معرفته لكي تغير قيم I_rel إلى المقياس المطلق، ولكن الموضوع لا يتم بهذه البساطة لسببين أولهما أن قيم F ليست ثابتة ولكنها تتغير بتغير λ/θsin. ولذلك قيم ̅I_abs̅ تتغير هي الأخرى مع تغير λ/θsin وهذا التغير عادة يؤخذ في الاعتبار ولذلك يقسم الفضاء العكسي reciprocal space إلى قشيرات متحدة المركز ورقيقة السمك بحيث إن التغير في قيمة F مع λ/θsin خلال كل قشرة يمكن إهماله ثم يحسب المتوسط لقيم I_rel من الانعكاسات في كل قشرة على حدة، وهذه القيم لـ I_rel̅ يمكن أن تقارن بعد ذلك مع القيم المحسوبة ̅I_abs̅ من قيم F الخاصة بكل قشرة.

أما المشكلة الثانية وهي الأخطر فهي أن قيم f's اللازمة للمعادلة (18-7) هي تلك القيم التي تصف الذرات كما هي في البلورة أي أنها تتذبذب بفعل الحرارة ولذلك يجب أن تتحد المعادلتان (17-7)، (18-7).

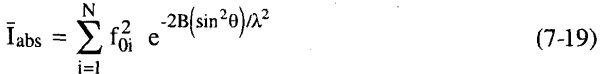
ولتعيين قيمة B نفترض أن لها نفس القيمة لكل الذرات ...

وهكذا إذا تم حساب الجانب الأيسر من المعادلة لكل قشرة لها القيم الثابتة. انظر شكل (7-4).

شكل (7-4)

طريقة ويلسون لتعيين معامل القياس والمعامل الحراري