Autosegmental contours

A resolution of this problem was set forth in Goldsmith 1976, who proposed that tones be given an autonomous representation from the rest of the segment, so that regular segments would be represented at one level and tones would be at another level, with the two levels of representation being synchronized via association lines. This theory, known as autosegmental phonology, posited representations such as those in (8).

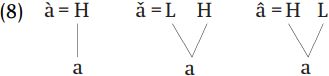
The representation of [á] simply says that when the rest of the vocal tract is in the configuration for the vowel [a], the vocal folds should be vibrating at a high rate as befits an H tone. The representation for [a˘] on the other hand says that while the rest of the vocal tract is producing the short vowel [a], the larynx should start vibrating slowly (produce an L tone), and then change to a higher rate of vibration to match that specified for an H tone – this produces the smooth increase in pitch which we hear as a rising tone. The representation of [â] simply reverses the order of the tonal specifications.

The view which autosegmental phonology takes of rules is different from that taken in the classical segmental theory. Rather than viewing the processes in (2) as being random changes in feature values, autosegmental theory views these operations as being adjustments in the temporal relations between the segmental tier and the tonal tier. Thus the change in (2a) where H becomes rising after L and fall can be expressed as (9).

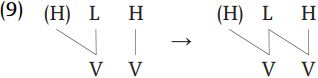
By simply adding an association between the L tone element on the left and the vowel which stands to the right, we are able to express this tonal change, without changing the intrinsic feature content of the string: we change only the timing relation between tones and vowels. This is notated as in (10), where the dashed association line means “insert an association line.”

Two other notational conventions are needed to understand the formulation of autosegmental rules. First, the deletion of an association line is indicated by crossing out the line:

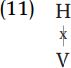
Second, an element (tone or vowel) which has no corresponding association on the other tier (vowel or tone) is indicated with the mark [ˊ], thus Vˊ indicates a toneless vowel and Hˊ indicates an H not linked to a vowel.

One striking advantage of the autosegmental model is that it allows us to express this common tonal process in a very simple way. The theory also allows each of the remaining processes in (2) to be expressed equally simply – in fact, essentially identically as involving an expansion of the temporal domain of a tone either to the left or to the right.

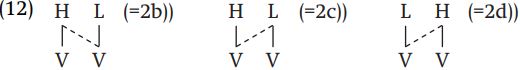
The problem of the natural classes formed by contour tones and level tones was particularly vexing for the linear theory. Most striking was the fact that what constitutes a natural class for contour tones depends on the linear order of the target and conditioning tones. If the conditioning tones stand on the left, then the natural classes observed are {L,F} and {H,R}, and if the conditioning tones stand on the right, then the natural groupings are {L,R} and {H,F}. In all other cases, the groupings of elements into natural classes are independent of whether the target is to the right or the left of the trigger. The autosegmental representation of contour tones thus provides a very natural explanation of what is otherwise a quite bizarre quirk in the concept “natural class.”

The autosegmental model also provides a principled explanation for the nonexistence of rules such as (4), i.e. the rules H ! F / {L,R} _ and L ! R / {H,F} _. The change of H to F after L would involve not just an adjustment in the temporal organization of an L-H sequence, but would necessitate the insertion of a separate L to the right of the H tone, which would have no connection with the preceding L; the change of H to F after R is even worse in that the change involves insertion of L when H is remotely preceded by a L. Thus, the closest that one could come to formalizing such a rule in the autosegmental approach would be as in (13).

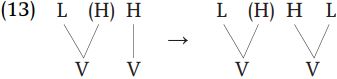
As we will discuss, autosegmental theory resulted in a considerable reconceptualization of phonological processes, and the idea that rules should be stated as insertions and deletions of association relationships made it impossible to express certain kinds of arbitrary actions, such as that of (13).

In addition to the fact that the theory provides a much-needed account of contour tones, quite a number of other arguments can be given for the autosegmental theory of tone. The essential claim of the theory is that there is not a one-to-one relation between the number of tones in an utterance and the number of vowels: a single tone can be associated with multiple vowels, or a single vowel can have multiple tones. Moreover, an operation on one tier, such as the deletion of a vowel, does not entail a corresponding deletion on the other tier. We will look at a number of arguments for the autonomy of tones and the vowels which phonetically bear them.