


 الجغرافية الطبيعية
الجغرافية الطبيعية 
 الجغرافية الحيوية
الجغرافية الحيوية 
 جغرافية التضاريس
جغرافية التضاريس 
 الجغرافية البشرية
الجغرافية البشرية 
 الجغرافية الاجتماعية
الجغرافية الاجتماعية 
 الجغرافية الاقتصادية
الجغرافية الاقتصادية 
 الاتجاهات الحديثة في الجغرافية
الاتجاهات الحديثة في الجغرافية | أهم أساليب تصنيف البيانات المستخدمة في إعداد خرائط الكوروبلث – التوزيعات المنحازة |
|
|
|
أقرأ أيضاً
التاريخ: 20-12-2020
التاريخ: 26-3-2022
التاريخ: 28-3-2022
التاريخ: 28-10-2020
|
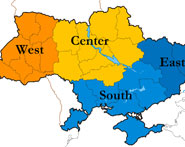
التوزيعات المنحازة Skewed Distribution:
عادة ما يكون توزيع قيم البيانات غير طبيعي، ويمكن أن تكون منحازة باتجاه معين، أو قد تظهر فجوات في التوزيع التكراري. هذه الأنواع من التوزيعات يمكن تصنيفها باستخدام فئات تعتمد على أرقام مدورة مناسبة Convenient Round Numbers رياضية Mathematic أو متوالية هندسية Geometric Series . تستخدم الأرقام المدورة لضمان تغطية الفئات لمدى قيم البيانات دون وجود فئات فارغة. فمثلا لو كانت معظم القيم مركزة في النهاية الدنيا للتوزيع ولكن بعض القيم مبعثرة ومنتشرة على مدى واسع نستطيع هنا تعديل مدى الفئات باستخدام مدى ضيق للفئات في حالة وجود تكرارات كثيرة للمشاهدات، أو استخدام مدى واسع للفئات في حالة وجود مشاهدات قليلة. باستخدام الأرقام المدورة المناسبة للفئات، يتحتم تحديد الفئات ليصبح 0-5، 5-10، 10-20، 20-50 ، 50-100.
إن هذا الأسلوب يمكن أن يكون فعالا عندما تكون البيانات منحازة وغير موزعة طبيعياً، ويجعل من المقارنات امراً صعباً. هناك أسلوب آخر للتعامل مع التوزيعات المنحازة يقوم على بناء الفئات على متوالية رياضية أو هندسية. للحصول على متوالية رياضية نحدد مدى الفئة الأصغر، ثم نزيد المدى للفئات التالية بإضافة قيمة ثابتة. فمثلاً يمكن أن نستخدم مدى فئة يساوي 7 لأصغر فئة، ثم نزيد المدى بمقدار 7 لكل فئة من الفئات التالية، فتصبح الفئات الناتجة 7-0، 21-7، 42-21، 70-42، 105-70. أما إذا كان توزيع القيم منحازا بشكل كبير، فيتحتم استخدام متوالية هندسيةGeometric Series ، وبالطريقة السابقة نفسها نختار مدى للفئة الدنيا، ثم نزيد المدى للفئات التالية بضرب المدى بثابت معين. فمثلاً، إذا بدأنا بمدى فئة يساوي 4 وضاعفنا المدى لكل فئة تالية، فإن الفئات الناتجة تكون 0-4 ، 4-12 ، 12-28 ، 28-60 ، 60-124.
|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|