


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-12-2021
Date: 11-1-2022
Date: 14-2-2017
|
"Implies" is the connective in propositional calculus which has the meaning "if 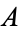 is true, then
is true, then 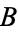 is also true." In formal terminology, the term conditional is often used to refer to this connective (Mendelson 1997, p. 13). The symbol used to denote "implies" is
is also true." In formal terminology, the term conditional is often used to refer to this connective (Mendelson 1997, p. 13). The symbol used to denote "implies" is 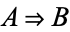 ,
, 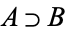 (Carnap 1958, p. 8; Mendelson 1997, p. 13), or
(Carnap 1958, p. 8; Mendelson 1997, p. 13), or 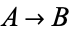 .
.
The Wolfram Language command Implies[p, q] can be used to represent the logical implication 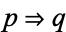 .
.
In classical logic, 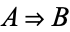 is an abbreviation for
is an abbreviation for 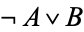 , where
, where 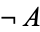 denotes NOT and
denotes NOT and 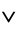 denoted OR (though this is not the case, for example, in intuitionistic logic).
denoted OR (though this is not the case, for example, in intuitionistic logic). 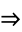 is a binary operator that is implemented in the Wolfram Language as Implies[A, B], and can not be extended to more than two arguments.
is a binary operator that is implemented in the Wolfram Language as Implies[A, B], and can not be extended to more than two arguments.
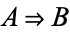 has the following truth table (Carnap 1958, p. 10; Mendelson 1997, p. 13).
has the following truth table (Carnap 1958, p. 10; Mendelson 1997, p. 13).
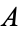 |
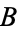 |
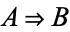 |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
If 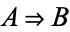 and
and 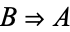 (i.e.,
(i.e., 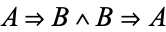 ), then
), then 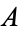 and
and 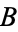 are said to be equivalent, a relationship which is written symbolically as
are said to be equivalent, a relationship which is written symbolically as  ,
, 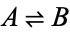 , or
, or 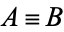 (Carnap 1958, p. 8).
(Carnap 1958, p. 8).
REFERENCES:
Carnap, R. Introduction to Symbolic Logic and Its Applications. New York: Dover, p. 8, 1958.
Mendelson, E. Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|