تاريخ الرياضيات
الاعداد و نظريتها
تاريخ التحليل
تار يخ الجبر
الهندسة و التبلوجي
الرياضيات في الحضارات المختلفة
العربية
اليونانية
البابلية
الصينية
المايا
المصرية
الهندية
الرياضيات المتقطعة
المنطق
اسس الرياضيات
فلسفة الرياضيات
مواضيع عامة في المنطق
الجبر
الجبر الخطي
الجبر المجرد
الجبر البولياني
مواضيع عامة في الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
الهندسة المستوية
الهندسة غير المستوية
مواضيع عامة في الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
معادلات تفاضلية
معادلات تكاملية
مواضيع عامة في المعادلات
التحليل
التحليل العددي
التحليل العقدي
التحليل الدالي
مواضيع عامة في التحليل
التحليل الحقيقي
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
500AD
500-1499
1000to1499
1500to1599
1600to1649
1650to1699
1700to1749
1750to1779
1780to1799
1800to1819
1820to1829
1830to1839
1840to1849
1850to1859
1860to1864
1865to1869
1870to1874
1875to1879
1880to1884
1885to1889
1890to1894
1895to1899
1900to1904
1905to1909
1910to1914
1915to1919
1920to1924
1925to1929
1930to1939
1940to the present
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان
Building Problem
المؤلف:
Bhatti, M. A
المصدر:
Practical Optimization Methods with Mathematica Applications. New York: Springer-Verlag, 2000.
الجزء والصفحة:
...
15-12-2021
1143
+
-
20
Building Problem
A hypothetic building design problem in optimization with constraints proposed by Bhatti (2000, pp. 3-5). To save energy costs for heating and cooling, an architect wishes to design a cuboidal building that is partially underground. Let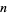 
be the number of stories (which therefore must be a positive integer), 
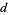the depth of the building below ground, 
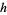the height of the building above ground, 
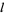the length of the building, and 
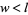the width of the building. The floor space needed is at least 
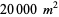, the lot size requires that 
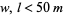, the building shape is specified so that 
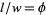(the golden ratio, approximately 1.618), each story is 3.5 m high, heating and cooling costs are estimated at 
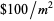for exposed surface of the building, and it has been specified that annual climate control costs should not exceed 
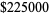. The problem then asks to minimize the volume that must be excavated to build the building.
This is equivalent to minimizing the function
 |
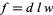(1) |
subject to the constraints
 |
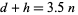(2) |
 |
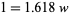(3) |
 |
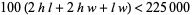(4) |
 |
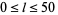(5) |
 |
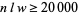(6) |
 |
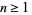(7) |
 |
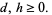(8) |
There is a fairly large region of parameter spacing giving near-optimal solution (and all well within the specified precision of the problem), with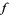 
minimized near 
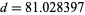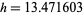m, 
m,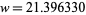 
m, (corresponding to 
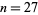and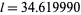 
), giving 
.
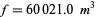REFERENCES:
Bhatti, M. A. Practical Optimization Methods with Mathematica Applications. New York: Springer-Verlag, 2000.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
الآخبار الصحية
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
