


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-12-2021
Date: 14-12-2021
Date: 14-12-2021
|
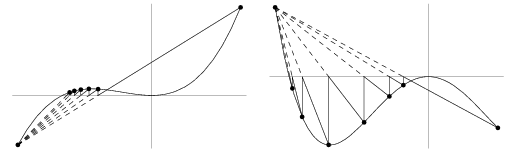
An algorithm for finding roots which retains that prior estimate for which the function value has opposite sign from the function value at the current best estimate of the root. In this way, the method of false position keeps the root bracketed (Press et al. 1992).
Using the two-point form of the line
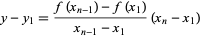 |
with 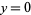 , using
, using 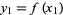 , and solving for
, and solving for 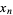 therefore gives the iteration
therefore gives the iteration
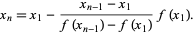 |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 18, 1972.
Chabert, J.-L. (Ed.). "Methods of False Position." Ch. 3 in A History of Algorithms: From the Pebble to the Microchip. New York: Springer-Verlag, pp. 83-112, 1999.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Secant Method, False Position Method, and Ridders' Method." §9.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 347-352, 1992.
Whittaker, E. T. and Robinson, G. "The Rule of False Position." §49 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 92-94, 1967.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|