


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-10-2021
Date: 22-8-2021
Date: 2-10-2021
|
Wavelets are a class of a functions used to localize a given function in both space and scaling. A family of wavelets can be constructed from a function 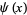 , sometimes known as a "mother wavelet," which is confined in a finite interval. "Daughter wavelets"
, sometimes known as a "mother wavelet," which is confined in a finite interval. "Daughter wavelets" 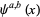 are then formed by translation (
are then formed by translation (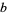 ) and contraction (
) and contraction (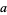 ). Wavelets are especially useful for compressing image data, since a wavelet transform has properties which are in some ways superior to a conventional Fourier transform.
). Wavelets are especially useful for compressing image data, since a wavelet transform has properties which are in some ways superior to a conventional Fourier transform.
An individual wavelet can be defined by
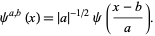 |
(1) |
Then
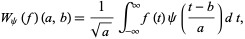 |
(2) |
and Calderón's formula gives
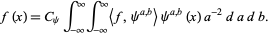 |
(3) |
A common type of wavelet is defined using Haar functions.
REFERENCES:
Benedetto, J. J. and Frazier, M. (Eds.). Wavelets: Mathematics and Applications. Boca Raton, FL: CRC Press, 1994.
Chui, C. K. An Introduction to Wavelets. San Diego, CA: Academic Press, 1992.
Chui, C. K. (Ed.). Wavelets: A Tutorial in Theory and Applications. San Diego, CA: Academic Press, 1992.
Chui, C. K.; Montefusco, L.; and Puccio, L. (Eds.). Wavelets: Theory, Algorithms, and Applications. San Diego, CA: Academic Press, 1994.
Daubechies, I. Ten Lectures on Wavelets. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1992.
Erlebacher, G. H.; Hussaini, M. Y.; and Jameson, L. M. (Eds.). Wavelets: Theory and Applications. New York: Oxford University Press, 1996.
Foufoula-Georgiou, E. and Kumar, P. (Eds.). Wavelets in Geophysics. San Diego, CA: Academic Press, 1994.
Hernández, E. and Weiss, G. A First Course on Wavelets. Boca Raton, FL: CRC Press, 1996.
Hubbard, B. B. The World According to Wavelets: The Story of a Mathematical Technique in the Making, 2nd rev. upd. ed. New York: A K Peters, 1998.
Jawerth, B. and Sweldens, W. "An Overview of Wavelet Based Multiresolution Analysis." SIAM Rev. 36, 377-412, 1994.
Kaiser, G. A Friendly Guide to Wavelets. Cambridge, MA: Birkhäuser, 1994.
Massopust, P. R. Fractal Functions, Fractal Surfaces, and Wavelets. San Diego, CA: Academic Press, 1994.
Meyer, Y. Wavelets: Algorithms and Applications. Philadelphia, PA: SIAM Press, 1993.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Wavelet Transforms." §13.10 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 584-599, 1992.
Resnikoff, H. L. and Wells, R. O. J. Wavelet Analysis: The Scalable Structure of Information. New York: Springer-Verlag, 1998.
Schumaker, L. L. and Webb, G. (Eds.). Recent Advances in Wavelet Analysis. San Diego, CA: Academic Press, 1993.
Stollnitz, E. J.; DeRose, T. D.; and Salesin, D. H. "Wavelets for Computer Graphics: A Primer, Part 1." IEEE Computer Graphics and Appl. 15, No. 3, 76-84, 1995.
Stollnitz, E. J.; DeRose, T. D.; and Salesin, D. H. "Wavelets for Computer Graphics: A Primer, Part 2." IEEE Computer Graphics and Appl. 15, No. 4, 75-85, 1995.
Strang, G. "Wavelets and Dilation Equations: A Brief Introduction." SIAM Rev. 31, 614-627, 1989.
Strang, G. "Wavelets." Amer. Sci. 82, 250-255, 1994.
Taswell, C. Handbook of Wavelet Transform Algorithms. Boston, MA: Birkhäuser, 1996.
Teolis, A. Computational Signal Processing with Wavelets. Boston, MA: Birkhäuser, 1997.
Vidakovic, B. Statistical Modeling by Wavelets. New York: Wiley, 1999.
Walker, J. S. A Primer on Wavelets and their Scientific Applications. Boca Raton, FL: CRC Press, 1999.
Walter, G. G. Wavelets and Other Orthogonal Systems with Applications. Boca Raton, FL: CRC Press, 1994.
Weisstein, E. W. "Books about Wavelets." http://www.ericweisstein.com/encyclopedias/books/Wavelets.html.
Wickerhauser, M. V. Adapted Wavelet Analysis from Theory to Software. Wellesley, MA: Peters, 1994.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|