المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
مـرحلة إيـجاد القـدرة علـى الشـراء فـي سـلوك المـستـهلك
2024-11-22
مرحلـة خلـق الرغبـة علـى الشـراء فـي سلـوك المـستهـلك 2
2024-11-22
مراحل سلوك المستهلك كمحدد لقرار الشراء (مرحلة خلق الرغبة على الشراء1)
2024-11-22
عمليات خدمة الثوم بعد الزراعة
2024-11-22
زراعة الثوم
2024-11-22
تكاثر وطرق زراعة الثوم
2024-11-22

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
ماذا يعني إذن التخطيط الاستراتيجي
12-6-2019
الخـطـوات العـمليـة للتـوريـق
15/12/2022
حكم سجود المأموم على ظهر غيره إذا زوحم.
17-1-2016
Sonoporation
24-2-2020
ريتز ، ولتر
10-11-2015
الواجب الموقّت
30-8-2016

Flip Bifurcation  
  
1407   04:10 مساءً   date: 7-10-2021
Author : Rasband, S. N
Book or Source : Chaotic Dynamics of Nonlinear Systems. New York: Wiley
Page and Part : pp. 27-30


Read More
Euler Backward Method
Date: 24-11-2021 1462
Driver,s Licenses
Date: 11-2-2016 1218
Criss-Cross Method
Date: 15-12-2021 824

Flip Bifurcation

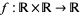Let f:R×R->R be a one-parameter family of 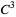C^3 maps satisfying

f(0,0) = 0

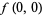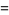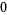(1)
[(partialf)/(partialx)]_(mu=0,x=0) = -1

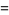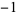(2)
[(partial^2f)/(partialx^2)]_(mu=0,x=0) < 0

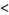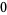(3)
[(partial^3f)/(partialx^3)]_(mu=0,x=0) < 0.

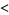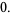(4)

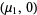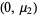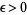Then there are intervals (mu_1,0), (0,mu_2), and epsilon>0 such that

1. If 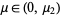mu in (0,mu_2), then 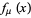f_mu(x) has one unstable fixed point and one stable orbit of period two for 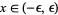x in (-epsilon,epsilon), and

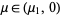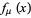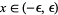2. If mu in (mu_1,0), then f_mu(x) has a single stable fixed point for x in (-epsilon,epsilon).

This type of bifurcation is known as a flip bifurcation. An example of an equation displaying a flip bifurcation is

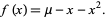f(x)=mu-x-x^2.

(5)

REFERENCES:

Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 27-30, 1990.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
التاريخ / 2024-11-18

الأخبار العلمية
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
التاريخ / 2024-11-18

الساحة الاسلامية
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
التاريخ / 2024-11-22