Sierpiński Curve

There are several fractal curves associated with Sierpiński.

The area for the first Sierpiński curve illustrated above (Sierpiński curve 1912) is

The curve is called the Sierpiński curve by Cundy and Rollett (1989, pp. 67-68), the Sierpiński's square snowflake by Wells (1991, p. 229), and is pictured but not named by Steinhaus (1999, pp. 102-103). The 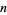th iteration of the first Sierpiński curve is implemented in the Wolfram Language as SierpinskiCurve[n].

The limit of the second Sierpiński's curve illustrated above has area

The Sierpiński arrowhead curve is another Sierpiński curve.

REFERENCES:

Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., 1989.

Dickau, R. M. "Two-Dimensional L-Systems." http://mathforum.org/advanced/robertd/lsys2d.html.

Gardner, M. Penrose Tiles and Trapdoor Ciphers... and the Return of Dr. Matrix, reissue ed. New York: W. H. Freeman, p. 34, 1989.

Sierpiński, W. "Sur une nouvelle courbe continue qui remplit toute une aire plane." Bull. l'Acad. des Sciences Cracovie A, 462-478, 1912.

Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, 1999.

Wagon, S. Mathematica in Action. New York: W. H. Freeman, p. 207, 1991.

Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 229, 1991.