Thurston's Geometrization Conjecture

Thurston's conjecture proposed a complete characterization of geometric structures on three-dimensional manifolds.

Before stating Thurston's geometrization conjecture in detail, some background information is useful. Three-dimensional manifolds possess what is known as a standard two-level decomposition. First, there is the connected sum decomposition, which says that every compact three-manifold is the connected sum of a unique collection of prime three-manifolds.

The second decomposition is the Jaco-Shalen-Johannson torus decomposition, which states that irreducible orientable compact 3-manifolds have a canonical (up to isotopy) minimal collection of disjointly embedded incompressible tori such that each component of the 3-manifold removed by the tori is either "atoroidal" or "Seifert-fibered."

Thurston's conjecture is that, after you split a three-manifold into its connected sum and the Jaco-Shalen-Johannson torus decomposition, the remaining components each admit exactly one of the following geometries:

1. Euclidean geometry,

2. Hyperbolic geometry,

3. Spherical geometry,

4. The geometry of ,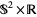

5. The geometry of ,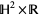

6. The geometry of the universal cover 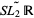 of the Lie group ,

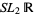7. Nil geometry, or

8. Sol geometry.

Here, 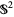 is the 2-sphere (in a topologist's sense) and  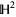is the hyperbolic plane. If Thurston's conjecture is true, the truth of the Poincaré conjecture immediately follows. Thurston shared the 1982 Fields Medal for work done in proving that the conjecture held in a subset of these cases.

Six of these geometries are now well understood, and there has been a great deal of progress with hyperbolic geometry (the geometry of constant negative scalar curvature). However, the geometry of constant positive curvature is still poorly understood, and in this geometry, the Thurston elliptization conjecture extends the Poincaré conjecture (Milnor).

Results due to Perelman (2002, 2003) appear to establish the geometrization conjecture, and thus also the Poincaré conjecture. Unlike a number of previous manuscripts attempting to prove the Poincaré conjecture, mathematicians familiar with Perelman's work describe it as well thought-out and expect that it will be difficult to locate any mistakes (Robinson 2003).

REFERENCES:

Anderson, M. T. "Scalar Curvature and Geometrization Conjectures for 3-Manifolds." MSRI Publ. 30, 1997. https://www.math.sunysb.edu/~anderson/.

Collins, G. P. "The Shapes of Space." Sci. Amer. 291, 94-103, July 2004.

Milnor, J. "The Poincaré Conjecture." https://www.claymath.org/millennium/Poincare_Conjecture/Official_Problem_Description.pdf.

Milnor, J. Collected Papers, Vol. 2: The Fundamental Group. Publish or Perish Press, p. 93, 1995.

Perelman, G. "The Entropy Formula for the Ricci Flow and Its Geometric Application" 11 Nov 2002. https://arxiv.org/abs/math.DG/0211159.

Perelman, G. "Ricci Flow with Surgery on Three-Manifolds" 10 Mar 2003. https://arxiv.org/abs/math.DG/0303109.

Robinson, S. "Russian Reports He Has Solved a Celebrated Math Problem." The New York Times, p. D3, April 15, 2003.

Thurston, W. P. "Three-Dimensional Manifolds, Kleinian Groups and Hyperbolic Geometry." Bull. Amer. Math. Soc. 6, 357-381, 1982.

Weisstein, E. W. "Poincaré Conjecture Proved--This Time for Real." MathWorld Headline News, Apr. 15, 2003. https://mathworld.wolfram.com/news/2003-04-15/poincare/.