Productive Property

A property that is always fulfilled by the product of topological spaces, if it is fulfilled by each single factor. Examples of productive properties are connectedness, and path-connectedness, axioms 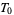, , 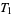 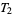and 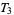, regularity and complete regularity, the property of being a Tychonoff space, but not axiom  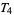and normality, which does not even pass, in general, from a space  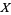to 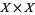. Metrizability is not productive, but is preserved by products of at most  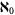spaces. Separability is not productive, but is preserved by products of at most  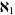spaces.

Compactness is productive by the Tychonoff theorem.

REFERENCES:

Joshi, K. D. "Productive Properties." §8.3 in Introduction to General Topology. New Delhi, India: Wiley, pp. 203-209, 1983.

Kelley, J. L. General Topology. New York: Van Nostrand, p. 133, 1955.