
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-6-2021
Date: 29-5-2021
Date: 11-5-2021
|
Let 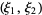 be a locally Euclidean coordinate system. Then
be a locally Euclidean coordinate system. Then
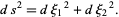 |
(1) |
Now plug in
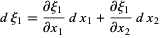 |
(2) |
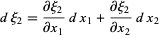 |
(3) |
to obtain
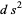 |
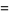 |
![[((partialxi_1)/(partialx_1))^2+((partialxi_2)/(partialx_1))^2]dx_1^2+2[(partialxi_1)/(partialx_1)(partialxi_1)/(partialx_2)+(partialxi_2)/(partialx_1)(partialxi_2)/(partialx_2)]dx_1dx_2+[((partialxi_1)/(partialx_2))^2+((partialxi_2)/(partialx_2))^2]dx_2^2.](https://mathworld.wolfram.com/images/equations/PlanarSpace/Inline4.gif) |
(4) |
Reading off the coefficients from
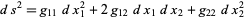 |
(5) |
gives
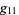 |
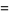 |
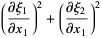 |
(6) |
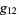 |
 |
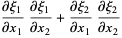 |
(7) |
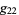 |
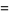 |
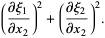 |
(8) |
Making a change of coordinates 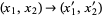 gives
gives
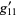 |
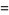 |
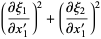 |
(9) |
 |
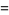 |
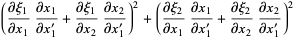 |
(10) |
 |
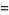 |
 |
(11) |
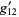 |
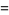 |
 |
(12) |
 |
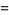 |
 |
(13) |
 |
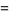 |
 |



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
العتبة العباسية المقدسة تُطلق فعّاليات مؤتمر ذاكرة الألم في العراق
|
|
|