Euclidean Space

Euclidean 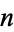-space, sometimes called Cartesian space or simply 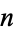-space, is the space of all n-tuples of real numbers, (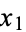, , 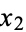..., 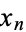). Such 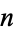-tuples are sometimes called points, although other nomenclature may be used (see below). The totality of 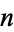-space is commonly denoted 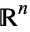, although older literature uses the symbol  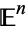(or actually, its non-doublestruck variant 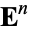; O'Neill 1966, p. 3).

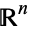 is a vector space and has Lebesgue covering dimension 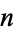. For this reason, elements of  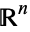are sometimes called 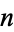-vectors.  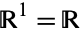is the set of real numbers (i.e., the real line), and  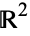is called the Euclidean plane. In Euclidean space, covariant and contravariant quantities are equivalent so .

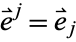REFERENCES:

Gray, A. "Euclidean Spaces." §1.1 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 2-5, 1997.

O'Neill, B. Elementary Differential Geometry. San Diego, CA: Academic Press, 1966.