
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-5-2021
Date: 19-6-2021
Date: 16-7-2021
|
Let the stick number 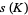 of a knot
of a knot 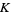 be the least number of straight sticks needed to make a knot
be the least number of straight sticks needed to make a knot 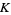 . The smallest stick number of any knot is
. The smallest stick number of any knot is 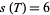 , where
, where 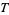 is the trefoil knot. If
is the trefoil knot. If 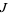 and
and 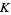 are knots, then
are knots, then
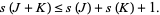 |
For a nontrivial knot 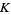 , let
, let 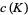 be the link crossing number (i.e., the least number of crossings in any projection of
be the link crossing number (i.e., the least number of crossings in any projection of 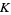 ). Then
). Then
![1/2[5+sqrt(25+8(c(K)-2))]<=s(K)<=2c(K).](https://mathworld.wolfram.com/images/equations/StickNumber/NumberedEquation2.gif) |
Stick numbers are implemented in the Wolfram Language as KnotData[knot, "StickNumber"].
The following table gives the stick number for knots on 10 or fewer crossings.
 |
3 | 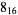 |
9 | 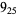 |
11 | 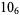 |
12 | 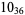 |
11 | 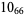 |
12 | 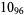 |
11 | 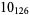 |
11 | 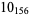 |
10 |
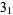 |
6 | 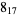 |
9 | 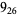 |
10 | 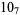 |
12 | 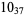 |
12 | 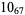 |
11 | 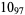 |
12 | 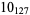 |
10 |  |
10 |
 |
7 |  |
9 |  |
11 | 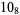 |
12 | 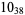 |
12 | 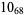 |
12 | 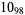 |
11 | 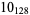 |
10 | 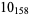 |
10 |
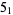 |
8 | 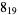 |
8 | 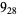 |
10 | 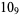 |
11 | 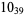 |
13 | 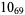 |
11 | 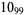 |
11 | 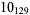 |
10 | 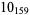 |
10 |
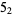 |
8 | 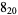 |
8 | 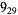 |
9 | 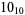 |
12 | 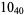 |
11 |  |
12 |  |
12 |  |
10 |  |
10 |
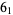 |
8 | 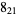 |
9 | 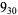 |
10 | 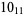 |
11 | 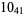 |
11 | 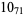 |
12 | 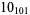 |
12 | 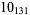 |
11 | 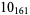 |
10 |
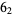 |
8 | 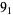 |
10 | 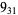 |
10 | 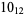 |
11 | 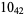 |
11 | 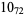 |
12 | 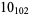 |
10 | 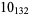 |
10 | 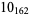 |
10 |
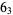 |
8 | 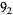 |
11 | 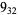 |
10 | 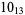 |
11 | 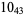 |
12 | 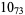 |
13 | 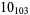 |
11 | 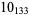 |
11 | 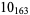 |
10 |
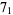 |
9 | 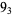 |
11 | 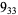 |
10 | 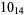 |
11 | 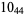 |
12 | 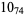 |
12 | 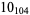 |
10 | 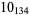 |
10 | 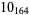 |
11 |
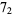 |
9 | 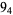 |
10 | 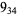 |
9 | 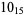 |
12 | 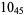 |
11 | 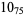 |
12 | 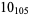 |
12 | 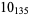 |
10 | 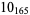 |
10 |
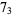 |
9 | 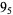 |
10 | 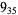 |
10 | 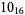 |
11 | 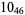 |
12 | 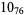 |
13 | 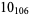 |
11 | 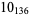 |
10 | ||
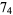 |
9 | 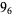 |
11 | 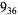 |
11 | 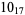 |
11 | 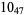 |
12 | 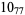 |
12 | 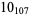 |
10 | 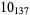 |
11 | ||
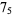 |
9 | 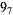 |
10 | 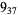 |
10 | 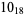 |
12 | 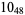 |
10 | 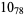 |
12 | 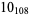 |
10 | 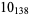 |
11 | ||
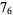 |
9 | 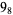 |
10 | 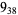 |
10 | 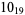 |
11 | 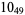 |
11 | 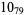 |
11 | 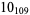 |
10 | 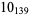 |
10 | ||
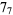 |
9 | 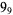 |
10 | 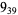 |
10 | 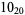 |
12 | 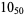 |
12 | 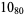 |
13 | 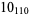 |
12 | 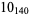 |
10 | ||
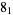 |
10 | 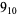 |
10 | 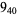 |
9 | 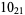 |
12 | 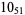 |
12 | 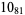 |
11 | 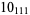 |
11 |  |
10 | ||
 |
10 |  |
11 |  |
9 | 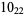 |
12 | 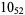 |
11 | 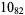 |
12 | 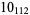 |
11 | 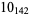 |
11 | ||
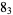 |
10 | 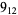 |
10 | 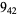 |
9 | 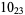 |
12 | 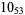 |
12 | 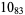 |
11 | 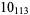 |
10 | 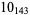 |
11 | ||
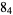 |
10 | 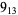 |
10 | 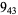 |
10 |  |
12 |  |
12 |  |
14 |  |
10 | 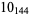 |
10 | ||
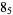 |
10 | 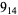 |
10 | 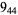 |
9 | 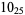 |
11 | 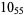 |
12 | 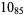 |
11 | 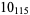 |
11 | 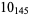 |
10 | ||
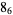 |
10 |  |
11 | 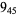 |
10 | 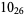 |
12 | 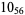 |
11 | 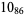 |
11 | 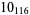 |
10 | 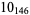 |
10 | ||
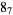 |
10 | 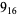 |
10 | 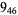 |
9 | 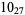 |
11 | 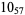 |
12 | 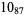 |
11 | 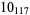 |
12 | 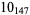 |
10 | ||
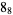 |
10 | 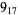 |
10 | 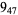 |
9 | 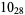 |
12 | 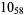 |
12 | 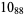 |
11 | 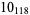 |
11 | 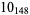 |
11 | ||
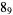 |
10 | 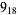 |
11 | 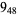 |
10 | 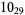 |
11 | 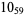 |
11 | 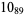 |
11 | 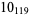 |
10 | 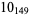 |
11 | ||
 |
10 |  |
10 |  |
9 |  |
12 | 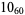 |
11 | 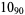 |
11 | 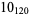 |
10 | 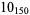 |
10 | ||
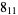 |
10 | 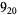 |
10 | 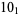 |
11 | 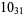 |
12 | 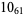 |
11 | 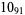 |
11 | 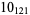 |
10 | 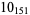 |
10 | ||
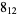 |
10 | 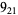 |
11 | 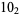 |
11 | 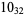 |
11 | 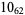 |
12 | 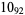 |
11 | 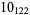 |
10 | 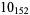 |
11 | ||
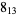 |
10 | 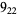 |
10 | 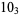 |
12 | 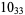 |
11 | 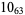 |
11 | 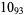 |
11 | 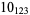 |
11 | 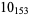 |
11 | ||
 |
10 |  |
11 |  |
11 |  |
12 |  |
13 |  |
11 |  |
10 |  |
11 | ||
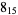 |
10 | 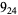 |
10 | 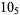 |
11 | 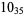 |
12 | 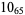 |
12 | 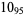 |
12 | 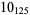 |
10 | 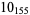 |
10 |
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 27-30, 1994.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|