Morton-Franks-Williams Inequality

Let 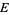 be the largest and  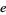the smallest power of  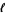in the HOMFLY polynomial of an oriented link, and  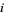be the braid index. Then the Morton-Franks-Williams inequality holds,

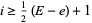(Morton 1986, 1988, Franks and Williams 1987). The inequality is sharp for all prime knots up to 10 crossings with the exceptions of 09-042, 09-049, 10-132, 10-150, and 10-156.

REFERENCES:

Franks, J. and Williams, R. F. "Braids and the Jones Polynomial." Trans. Amer. Math. Soc. 303, 97-108, 1987.

Morton, H. R. "Seifert Circles and Knot Polynomials." Math. Proc. Cambridge Philos. Soc. 99, 107-109, 1986.

Morton, H. R. "Polynomials from Braids." In Proceedings of the AMS-IMS-SIAM Joint Summer Research Conference in Mathematical Sciences on Artin's Braid Group held at the University of California, Santa Cruz, California, July 13-26, 1986 (Ed. J. S. Birman and A. Libgober). Providence, RI: Amer. Math. Soc., pp. 575-585, 1988.