


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-6-2021
Date: 12-8-2021
Date: 1-8-2021
|
In the usual diagram of inclusion homomorphisms, if the upper two maps are injective, then so are the other two.
More formally, consider a space 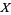 which is expressible as the union of pathwise-connected open sets
which is expressible as the union of pathwise-connected open sets 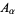 , each containing the basepoint
, each containing the basepoint 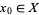 such that each intersection
such that each intersection 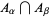 is pathwise-connected. Then, the homomorphism induced by the inclusion map from the free product of the fundamental groups of the
is pathwise-connected. Then, the homomorphism induced by the inclusion map from the free product of the fundamental groups of the 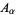 s to the fundamental group of
s to the fundamental group of 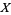 , i.e.,
, i.e.,
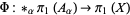 |
(1) |
is surjective (Hatcher 2001, p. 43). In addition, if each intersection 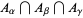 is pathwise-connected, then the kernel of
is pathwise-connected, then the kernel of 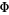 is the normal subgroup
is the normal subgroup 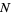 generated by all elements of the form
generated by all elements of the form
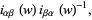 |
(2) |
where 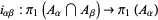 is the homomorphism induced by the inclusion
is the homomorphism induced by the inclusion 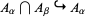 , and so
, and so 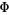 induces an isomorphism
induces an isomorphism
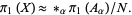 |
(3) |
REFERENCES:
Dodson, C. T. J. and Parker, P. E. A User's Guide to Algebraic Topology. Dordrecht, Netherlands: Kluwer, p. 88, 1997.
Hatcher, A. Algebraic Topology. Cambridge, England: Cambridge University Press, 2001.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 74-75 and 369-373, 1976.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|