F-Distribution

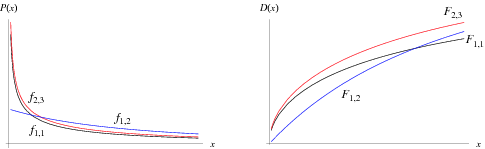
A continuous statistical distribution which arises in the testing of whether two observed samples have the same variance. Let 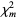 and 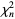 be independent variates distributed as chi-squared with  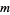and 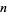 degrees of freedom.

Define a statistic 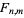 as the ratio of the dispersions of the two distributions

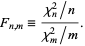(1)

This statistic then has an 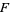-distribution on domain  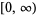with probability function  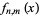and cumulative distribution function  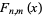given by

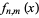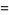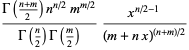			(2)
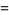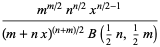			(3)
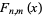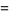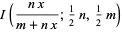			(4)
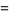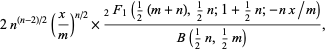			(5)

where 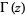 is the gamma function,  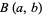is the beta function,  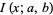is the regularized beta function, and  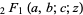is a hypergeometric function.

The 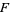-distribution is implemented in the Wolfram Language as FRatioDistribution[n, m].

The mean, variance, skewness and kurtosis excess are

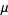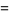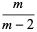			(6)
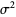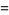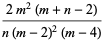			(7)
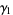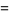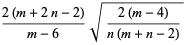			(8)
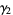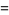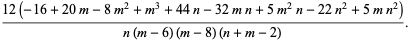			(9)

The probability that 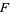 would be as large as it is if the first distribution has a smaller variance than the second is denoted .

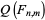REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 946-949, 1972.

David, F. N. "The Moments of the 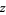 and 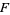 Distributions." Biometrika 36, 394-403, 1949.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Incomplete Beta Function, Student's Distribution, F-Distribution, Cumulative Binomial Distribution." §6.2 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 219-223, 1992.

Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 117-118, 1992.