


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-2-2021
Date: 27-3-2021
Date: 29-3-2021
|
A self-avoiding walk is a path from one point to another which never intersects itself. Such paths are usually considered to occur on lattices, so that steps are only allowed in a discrete number of directions and of certain lengths.

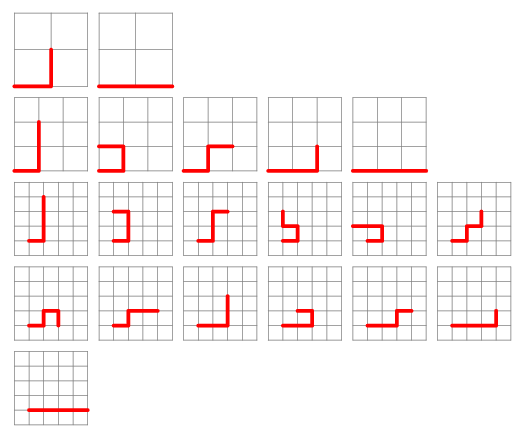
Consider a self-avoiding walk on a two-dimensional 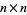 square grid (i.e., a lattice path which never visits the same lattice point twice) which starts at the origin, takes first step in the positive horizontal direction, and is restricted to nonnegative grid points only. The number of such paths of
square grid (i.e., a lattice path which never visits the same lattice point twice) which starts at the origin, takes first step in the positive horizontal direction, and is restricted to nonnegative grid points only. The number of such paths of  , 2, ... steps are 1, 2, 5, 12, 30, 73, 183, 456, 1151, ... (OEIS A046170).
, 2, ... steps are 1, 2, 5, 12, 30, 73, 183, 456, 1151, ... (OEIS A046170).
Similarly, consider a self-avoiding walk which starts at the origin, takes first step in the positive horizontal direction, is not restricted to nonnegative grid points only, but which is restricted to take an up step before taking the first down step. The number of such paths of 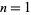 , 2, ... steps are 1, 2, 5, 13, 36, 98, 272, 740, 2034, ... (OEIS A046171).
, 2, ... steps are 1, 2, 5, 13, 36, 98, 272, 740, 2034, ... (OEIS A046171).
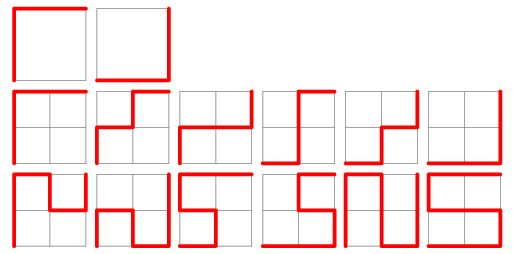
Self-avoiding rook walks are walks on an 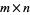 grid which start from
grid which start from 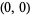 , end at
, end at 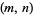 , and are composed of only horizontal and vertical steps. The following table gives the first few numbers
, and are composed of only horizontal and vertical steps. The following table gives the first few numbers 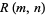 of such walks for small
of such walks for small 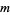 and
and 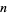 . The values for
. The values for 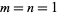 , 2, ... are 2, 12, 184, 8512, 1262816, ... (OEIS A007764).
, 2, ... are 2, 12, 184, 8512, 1262816, ... (OEIS A007764).
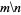 |
2 | 3 | 4 | 5 | 6 |
| 2 | 2 | ||||
| 3 | 4 | 12 | |||
| 4 | 8 | 38 | 184 | ||
| 5 | 16 | 125 | 976 | 8512 | |
| 6 | 32 | 414 | 5382 | 79384 | 1262816 |
There are a number of known formulas for computing 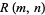 for small
for small 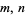 . For example,
. For example,
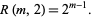 |
(1) |
There is a recurrence relation for 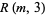 , given by
, given by 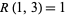 ,
, 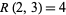 ,
, 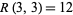 ,
, 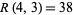 , and
, and
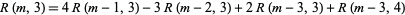 |
(2) |
for 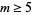 , as well as the generating function
, as well as the generating function
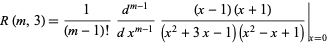 |
(3) |
(Abbott and Hanson 1978, Finch 2003).
A related sequence is the number of shapes which can be formed by bending a piece of wire of length 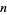 in the plane, where bends are of 0 or
in the plane, where bends are of 0 or 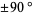 and the wire may cross itself at right angles but not pass over itself. The number of shapes for wires of length 1, 2, ... are 1, 2, 4, 10, 24, 66, 176, 493, ... (OEIS A001997).
and the wire may cross itself at right angles but not pass over itself. The number of shapes for wires of length 1, 2, ... are 1, 2, 4, 10, 24, 66, 176, 493, ... (OEIS A001997).
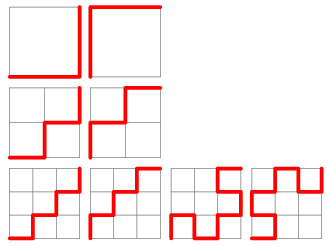
Consider a self-avoiding walk on a two-dimensional 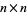 square grid from one corner to another such that no two consecutive steps are in the same direction. The number of such paths for
square grid from one corner to another such that no two consecutive steps are in the same direction. The number of such paths for 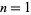 , 2, ... are 1, 2, 2, 4, 10, 36, 188, ... (OEIS A034165; counting the number of paths on the
, 2, ... are 1, 2, 2, 4, 10, 36, 188, ... (OEIS A034165; counting the number of paths on the 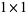 point "lattice" as 1), and the maximum lengths of these paths are 0, 2, 4, 10, 12, 26, 36, ... (OEIS A034166).
point "lattice" as 1), and the maximum lengths of these paths are 0, 2, 4, 10, 12, 26, 36, ... (OEIS A034166).
REFERENCES:
Abbott, H. L. and Hanson, D. "A Lattice Path Problem." Ars Combinatoria 6, 163-178, 1978.
Alm, S. E. "Upper Bounds for the Connective Constant of Self-Avoiding Walks." Combin. Prob. Comput. 2, 115-136, 1993.
Domb, C. "On Multiple Returns in the Random-Walk Problem." Proc. Cambridge Philos. Soc. 50, 586-591, 1954.
Domb, C. "Self-Avoiding Walks on Lattices." Adv. Chem. Phys. 15, 229-259, 1969.
Finch, S. R. "Self-Avoiding Walk Constants." §5.10 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 331-339, 2003.
Hayes, B. "How to Avoid Yourself." Amer. Sci. 86, 314-319, 1998.
Kesten, H. "On the Number of Self-Avoiding Walks." J. Math. Phys. 4, 960-969, 1963.
Lawler, G. F. Intersections of Random Walks. Boston, MA: Birkhäuser, 1991.
Sloane, N. J. A. Sequences A001997/M1206, A007764, A034165, A034166, A046170, and A046171 in "The On-Line Encyclopedia of Integer Sequences."
Whittington, S. G. and Guttman, A. J. "Self-Avoiding Walks which Cross a Square." J. Phys. A 23, 5601-5609, 1990.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|