Brownian Motion

A real-valued stochastic process 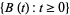 is a Brownian motion which starts at  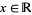if the following properties are satisfied:

1. .

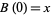2. For all times 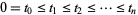, the increments 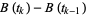, , 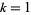..., 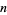, are independent random variables.

3. For all 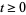, , 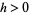the increments  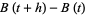are normally distributed with expectation value zero and variance .

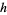4. The function 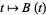 is continuous almost everywhere. The Brownian motion  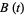is said to be standard if .

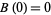It is easily shown from the above criteria that a Brownian motion has a number of unique natural invariance properties including scaling invariance and invariance under time inversion. Moreover, any Brownian motion 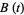 satisfies a law of large numbers so that

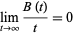almost everywhere. Moreover, despite looking ill-behaved at first glance, Brownian motions are Hölder continuous almost everywhere for all values 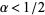. Contrarily, any Brownian motion is nowhere differentiable almost surely.

The above definition is extended naturally to get higher-dimensional Brownian motions. More precisely, given independent Brownian motions 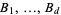 which start at 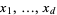, one can define a stochastic process  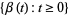by

Such a 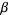 is called a 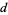-dimensional Brownian motion which starts at .

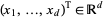REFERENCES:

Mörters, P. and Peres, Y. "Brownian Motion." 2008. http://www.stat.berkeley.edu/~peres/bmbook.pdf.