
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-2-2021
Date: 14-2-2016
Date: 28-3-2021
|
Bessel's correction is the factor 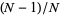 in the relationship between the variance
in the relationship between the variance 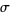 and the expectation values of the sample variance,
and the expectation values of the sample variance,
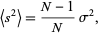 |
(1) |
where
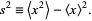 |
(2) |
As noted by Kenney and Keeping (1951, p. 161), the correction factor is probably more properly attributed to Gauss, who used it in this connection as early as 1823 (Gauss 1823).
For two samples,
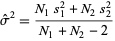 |
(3) |
(Kenney and Keeping 1951, p. 162).
REFERENCES:
Farebrother, R. W. Fitting Linear Relationships: A History of the Calculus of Observations 1750-1900. New York: Springer-Verlag, 1999.
Gauss, C. F. "Theoria combinationis obsevationum erroribus minimis obnoxiae." Werke, Vol. 4. Göttingen, Germany: p. 1, 1823.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
بالصور: ممثل المرجعية العليا الشيخ عبد المهدي الكربلائي يؤم جموع المؤمنين في صلاة عيد الفطر المبارك داخل الصحن الحسيني الشريف
|
|
|