Algebraic Number
المؤلف:
Conway, J. H. and Guy, R. K
المصدر:
"Algebraic Numbers." In The Book of Numbers. New York: Springer-Verlag
الجزء والصفحة:
...
30-1-2021
2303
Algebraic Number
If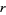 
is a root of a nonzero polynomial equation
 |
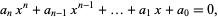(1)
|
where the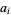 
s are integers (or equivalently, rational numbers) and 
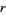satisfies no similar equation of degree 
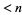, then 
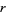is said to be an algebraic number of degree 
.
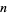A number that is not algebraic is said to be transcendental. If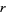 
is an algebraic number and 
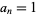, then it is called an algebraic integer.
In general, algebraic numbers are complex, but they may also be real. An example of a complex algebraic number is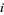 
, and an example of a real algebraic number is 
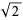, both of which are of degree 2.
The set of algebraic numbers is denoted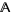 
(Wolfram Language), or sometimes 
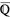(Nesterenko 1999), and is implemented in the Wolfram Language as Algebraics.
A number 
can then be tested to see if it is algebraic in the Wolfram Language using the command Element[x, Algebraics]. Algebraic numbers are represented in the Wolfram Language as indexed polynomial roots by the symbol Root[f, n], where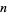 
is a number from 1 to the degree of the polynomial (represented as a so-called "pure function") 
.
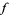Examples of some significant algebraic numbers and their degrees are summarized in the following table.
| constant |
degree |
Conway's constant  |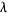
71 |
Delian constant  |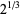
3 |
disk covering problem  |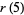
8 |
| Freiman's constant |
2 |
golden ratio  |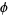
2 |
golden ratio conjugate  |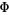
2 |
Graham's biggest little hexagon area  |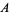
10 |
hard hexagon entropy constant  |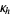
24 |
| heptanacci constant |
7 |
| hexanacci constant |
6 |
| i |
2 |
| Lieb's square ice constant |
2 |
logistic map 3-cycle onset  |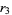
2 |
logistic map 4-cycle onset  |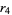
2 |
logistic map 5-cycle onset  |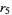
22 |
logistic map 6-cycle onset  |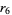
40 |
logistic map 7-cycle onset  |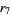
114 |
logistic map 8-cycle onset  |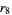
12 |
logistic map 16-cycle onset  |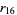
240 |
| pentanacci constant |
5 |
| plastic constant |
3 |
Pythagoras's constant  |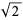
2 |
| silver constant |
3 |
| silver ratio |
2 |
| tetranacci constant |
4 |
| Theodorus's constant |
2 |
| tribonacci constant |
3 |
| twenty-vertex entropy constant |
2 |
| Wallis's constant |
3 |
If, instead of being integers, the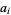 
s in the above equation are algebraic numbers 
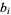, then any root of
 |
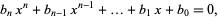(2)
|
is an algebraic number.
If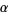 
is an algebraic number of degree 
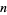satisfying the polynomial equation
 |
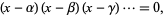(3)
|
then there are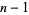 
other algebraic numbers 
, 
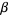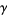, ... called the conjugates of 
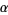. Furthermore, if 
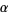satisfies any other algebraic equation, then its conjugates also satisfy the same equation (Conway and Guy 1996).
REFERENCES:
Conway, J. H. and Guy, R. K. "Algebraic Numbers." In The Book of Numbers. New York: Springer-Verlag, pp. 189-190, 1996.
Courant, R. and Robbins, H. "Algebraic and Transcendental Numbers." §2.6 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 103-107, 1996.
Ferreirós, J. "The Emergence of Algebraic Number Theory." §3.3 in Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Basel, Switzerland: Birkhäuser, pp. 94-99, 1999.
Hancock, H. Foundations of the Theory of Algebraic Numbers, Vol. 1: Introduction to the General Theory. New York: Macmillan, 1931.
Hancock, H. Foundations of the Theory of Algebraic Numbers, Vol. 2: The General Theory. New York: Macmillan, 1932.
Koch, H. Number Theory: Algebraic Numbers and Functions. Providence, RI: Amer. Math. Soc., 2000.
Nagell, T. Introduction to Number Theory. New York: Wiley, p. 35, 1951.
Narkiewicz, W. Elementary and Analytic Number Theory of Algebraic Numbers. Warsaw: Polish Scientific Publishers, 1974.
Nesterenko, Yu. V. A Course on Algebraic Independence: Lectures at IHP 1999. Unpublished manuscript. 1999.
Wagon, S. "Algebraic Numbers." §10.5 in Mathematica in Action. New York: W. H. Freeman, pp. 347-353, 1991.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
