المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Fibonacci Pseudoprime |
 1058
 04:59 مساءً
date: 24-1-2021 |
Author : Di Porto, A. 
Book or Source : "Nonexistence of Even Fibonacci Pseudoprimes of the First Kind." Fib. Quart. 31 
Page and Part : ...|
Read More
Date: 21-12-2020
2485
Date: 1-10-2020
620
Date: 24-11-2019
680
|
Consider a Lucas sequence with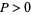 
and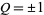 
. A Fibonacci pseudoprime is a composite number 
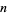such that
 |
There exist no even Fibonacci pseudoprimes with parameters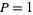 
and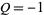 
(Di Porto 1993) or 
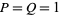(André-Jeannin 1996). André-Jeannin (1996) also proved that if 
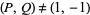and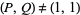 
, then there exists at least one even Fibonacci pseudoprime with parameters 
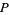and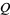 
.
REFERENCES:
André-Jeannin, R. "On the Existence of Even Fibonacci Pseudoprimes with Parameters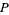 
and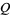 
." Fib. Quart. 34, 75-78, 1996.
Di Porto, A. "Nonexistence of Even Fibonacci Pseudoprimes of the First Kind." Fib. Quart. 31, 173-177, 1993.
Ribenboim, P. "Fibonacci Pseudoprimes." §2.X.A in The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, pp. 127-129, 1996.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
