Let 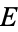 be an elliptic curve defined over the field of rationals  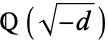having equation

with 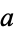 and 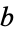 integers. Let  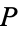be a point on  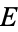with integer coordinates and having infinite order in the additive group of rational points of 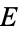, and let  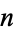be a composite natural number such that 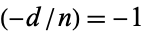, where  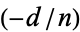is the Jacobi symbol. Then if

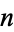 is called an elliptic pseudoprime for .

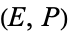REFERENCES:

Balasubramanian, R. and Murty, M. R. "Elliptic Pseudoprimes. II." In Séminaire de Théorie des Nombres, Paris 1988-1989 (Ed. C. Goldstein). Boston, MA: Birkhäuser, pp. 13-25, 1990.

Gordon, D. M. "The Number of Elliptic Pseudoprimes." Math. Comput. 52, 231-245, 1989.

Gordon, D. M. "Pseudoprimes on Elliptic Curves." In Number Theory--Théorie des nombres:Proceedings of the International Number Theory Conference Held at Université Laval in 1987 (Ed. J. M. DeKoninck and C. Levesque). Berlin: de Gruyter, pp. 290-305, 1989.

Miyamoto, I. and Murty, M. R. "Elliptic Pseudoprimes." Math. Comput. 53, 415-430, 1989.

Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, pp. 132-134, 1996.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد