


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-11-2020
Date: 20-8-2020
Date: 17-12-2020
|
A Mersenne prime is a Mersenne number, i.e., a number of the form
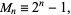 |
that is prime. In order for  to be prime,
to be prime,  must itself be prime. This is true since for composite
must itself be prime. This is true since for composite  with factors
with factors 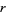 and
and 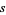 ,
, 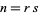 . Therefore,
. Therefore, 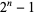 can be written as
can be written as 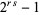 , which is a binomial number that always has a factor
, which is a binomial number that always has a factor 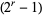 .
.
The first few Mersenne primes are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, ... (OEIS A000668) corresponding to indices 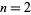 , 3, 5, 7, 13, 17, 19, 31, 61, 89, ... (OEIS A000043).
, 3, 5, 7, 13, 17, 19, 31, 61, 89, ... (OEIS A000043).
Mersenne primes were first studied because of the remarkable properties that every Mersenne prime corresponds to exactly one perfect number. L. Welsh maintains an extensive bibliography and history of Mersenne numbers.
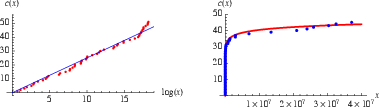
It has been conjectured that there exist an infinite number of Mersenne primes. Fitting a line through the origin to the asymptotic number of Mersenne primes 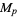 with
with 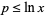 for the first 51 (known) Mersenne primes gives a best-fit line with
for the first 51 (known) Mersenne primes gives a best-fit line with 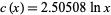 , illustrated above. If the line is not restricted to pass through the origin, the best fit is
, illustrated above. If the line is not restricted to pass through the origin, the best fit is  . It has been conjectured (without any particularly strong evidence) that the constant is given by
. It has been conjectured (without any particularly strong evidence) that the constant is given by  , where
, where  is the Euler-Mascheroni constant (Havil 2003, p. 116; Caldwell), a result related to Wagstaff's conjecture
is the Euler-Mascheroni constant (Havil 2003, p. 116; Caldwell), a result related to Wagstaff's conjecture

However, finding Mersenne primes is computationally very challenging. For example, the 1963 discovery that 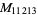 is prime was heralded by a special postal meter design, illustrated above, issued in Urbana, Illinois.
is prime was heralded by a special postal meter design, illustrated above, issued in Urbana, Illinois.
G. Woltman has organized a distributed search program via the Internet known as GIMPS (Great Internet Mersenne Prime Search) in which hundreds of volunteers use their personal computers to perform pieces of the search. The efforts of GIMPS volunteers make this distributed computing project the discoverer of all of the Mersenne primes discovered since late 1996. As of Sep. 24, 2020, GIMPS participants have tested and verified all exponents below 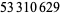 and tested all exponents below
and tested all exponents below 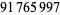 at least once (GIMPS).
at least once (GIMPS).
The table below gives the index 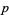 of known Mersenne primes (OEIS A000043)
of known Mersenne primes (OEIS A000043) 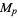 , together with the number of digits, discovery years, and discoverer. A similar table has been compiled by C. Caldwell. Note that sequential indexing of "the"
, together with the number of digits, discovery years, and discoverer. A similar table has been compiled by C. Caldwell. Note that sequential indexing of "the" 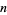 th Mersenne prime is tentative for
th Mersenne prime is tentative for 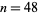 until all exponents between
until all exponents between  and
and 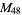 (namely up to
(namely up to 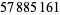 ) have been verified to be composite (and therefore also tentative for the other known Mersenne primes
) have been verified to be composite (and therefore also tentative for the other known Mersenne primes 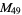 through
through 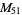 ).
).
| # | 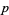 |
digits | year | discoverer (reference) | value |
| 1 | 2 | 1 | antiquity | 3 | |
| 2 | 3 | 1 | antiquity | 7 | |
| 3 | 5 | 2 | antiquity | 31 | |
| 4 | 7 | 3 | antiquity | 127 | |
| 5 | 13 | 4 | 1461 | Reguis (1536), Cataldi (1603) | 8191 |
| 6 | 17 | 6 | 1588 | Cataldi (1603) | 131071 |
| 7 | 19 | 6 | 1588 | Cataldi (1603) | 524287 |
| 8 | 31 | 10 | 1750 | Euler (1772) | 2147483647 |
| 9 | 61 | 19 | 1883 | Pervouchine (1883), Seelhoff (1886) | 2305843009213693951 |
| 10 | 89 | 27 | 1911 | Powers (1911) | 618970019642690137449562111 |
| 11 | 107 | 33 | 1913 | Powers (1914) | 162259276829213363391578010288127 |
| 12 | 127 | 39 | 1876 | Lucas (1876) | 170141183460469231731687303715884105727 |
| 13 | 521 | 157 | Jan. 30, 1952 | Robinson (1954) | 68647976601306097149...12574028291115057151 |
| 14 | 607 | 183 | Jan. 30, 1952 | Robinson (1954) | 53113799281676709868...70835393219031728127 |
| 15 | 1279 | 386 | Jun. 25, 1952 | Robinson (1954) | 10407932194664399081...20710555703168729087 |
| 16 | 2203 | 664 | Oct. 7, 1952 | Robinson (1954) | 14759799152141802350...50419497686697771007 |
| 17 | 2281 | 687 | Oct. 9, 1952 | Robinson (1954) | 44608755718375842957...64133172418132836351 |
| 18 | 3217 | 969 | Sep. 8, 1957 | Riesel | 25911708601320262777...46160677362909315071 |
| 19 | 4253 | 1281 | Nov. 3, 1961 | Hurwitz | 19079700752443907380...76034687815350484991 |
| 20 | 4423 | 1332 | Nov. 3, 1961 | Hurwitz | 28554254222827961390...10231057902608580607 |
| 21 | 9689 | 2917 | May 11, 1963 | Gillies (1964) | 47822027880546120295...18992696826225754111 |
| 22 | 9941 | 2993 | May 16, 1963 | Gillies (1964) | 34608828249085121524...19426224883789463551 |
| 23 | 11213 | 3376 | Jun. 2, 1963 | Gillies (1964) | 28141120136973731333...67391476087696392191 |
| 24 | 19937 | 6002 | Mar. 4, 1971 | Tuckerman (1971) | 43154247973881626480...36741539030968041471 |
| 25 | 21701 | 6533 | Oct. 30, 1978 | Noll and Nickel (1980) | 44867916611904333479...57410828353511882751 |
| 26 | 23209 | 6987 | Feb. 9, 1979 | Noll (Noll and Nickel 1980) | 40287411577898877818...36743355523779264511 |
| 27 | 44497 | 13395 | Apr. 8, 1979 | Nelson and Slowinski | 85450982430363380319...44867686961011228671 |
| 28 | 86243 | 25962 | Sep. 25, 1982 | Slowinski | 53692799550275632152...99857021709433438207 |
| 29 | 110503 | 33265 | Jan. 28, 1988 | Colquitt and Welsh (1991) | 52192831334175505976...69951621083465515007 |
| 30 | 132049 | 39751 | Sep. 20, 1983 | Slowinski | 51274027626932072381...52138578455730061311 |
| 31 | 216091 | 65050 | Sep. 6, 1985 | Slowinski | 74609310306466134368...91336204103815528447 |
| 32 | 756839 | 227832 | Feb. 19, 1992 | Slowinski and Gage | 17413590682008709732...02603793328544677887 |
| 33 | 859433 | 258716 | Jan. 10, 1994 | Slowinski and Gage | 12949812560420764966...02414267243500142591 |
| 34 | 1257787 | 378632 | Sep. 3, 1996 | Slowinski and Gage | 41224577362142867472...31257188976089366527 |
| 35 | 1398269 | 420921 | Nov. 12, 1996 | Joel Armengaud/GIMPS | 81471756441257307514...85532025868451315711 |
| 36 | 2976221 | 895832 | Aug. 24, 1997 | Gordon Spence/GIMPS | 62334007624857864988...76506256743729201151 |
| 37 | 3021377 | 909526 | Jan. 27, 1998 | Roland Clarkson/GIMPS | 12741168303009336743...25422631973024694271 |
| 38 | 6972593 | 2098960 | Jun. 1, 1999 | Nayan Hajratwala/GIMPS | 43707574412708137883...35366526142924193791 |
| 39 | 13466917 | 4053946 | Nov. 14, 2001 | Michael Cameron/GIMPS | 92494773800670132224...30073855470256259071 |
| 40 | 20996011 | 6320430 | Nov. 17, 2003 | Michael Shafer/GIMPS | 12597689545033010502...94714065762855682047 |
| 41 | 24036583 | 7235733 | May 15, 2004 | Josh Findley/GIMPS | 29941042940415717208...67436921882733969407 |
| 42 | 25964951 | 7816230 | Feb. 18, 2005 | Martin Nowak/GIMPS | 12216463006127794810...98933257280577077247 |
| 43 | 30402457 | 9152052 | Dec. 15, 2005 | Curtis Cooper and Steven Boone/GIMPS | 31541647561884608093...11134297411652943871 |
| 44 | 32582657 | 9808358 | Sep. 4, 2006 | Curtis Cooper and Steven Boone/GIMPS | 12457502601536945540...11752880154053967871 |
| 45 | 37156667 | 11185272 | Sep. 6, 2008 | Hans-Michael Elvenich/GIMPS | 20225440689097733553...21340265022308220927 |
| 46 | 42643801 | 12837064 | Jun. 12, 2009 | Odd Magnar Strindmo/GIMPS | 16987351645274162247...84101954765562314751 |
| 47 | 43112609 | 12978189 | Aug. 23, 2008 | Edson Smith/GIMPS | 31647026933025592314...80022181166697152511 |
| 48? | 57885161 | 17425170 | Jan. 25, 2013 | Curtis Cooper/GIMPS | 58188726623224644217...46141988071724285951 |
| 49? | 74207281 | 22338618 | Jan. 7, 2016 | Curtis Cooper/GIMPS | 30037641808460618205...87010073391086436351 |
| 50? | 77232917 | 23249425 | Dec. 26, 2017 | Jonathan Pace/GIMPS | 46733318335923109998...82730618069762179071 |
| 51? | 82589933 | 24862048 | Dec. 7, 2018 | Patrick Laroche/GIMPS | 14889444574204132554...37951210325217902591 |
Trial division is often used to establish the compositeness of a potential Mersenne prime. This test immediately shows 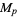 to be composite for
to be composite for 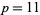 , 23, 83, 131, 179, 191, 239, and 251 (with small factors 23, 47, 167, 263, 359, 383, 479, and 503, respectively). A much more powerful primality test for
, 23, 83, 131, 179, 191, 239, and 251 (with small factors 23, 47, 167, 263, 359, 383, 479, and 503, respectively). A much more powerful primality test for 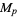 is the Lucas-Lehmer test.
is the Lucas-Lehmer test.
If 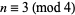 is a prime, then
is a prime, then 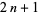 divides
divides 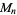 iff
iff 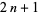 is prime. It is also true that prime divisors of
is prime. It is also true that prime divisors of 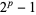 must have the form
must have the form 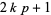 where
where 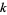 is a positive integer and simultaneously of either the form
is a positive integer and simultaneously of either the form 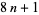 or
or 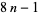 (Uspensky and Heaslet 1939).
(Uspensky and Heaslet 1939).
A prime factor 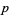 of a Mersenne number
of a Mersenne number 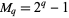 is a Wieferich prime iff
is a Wieferich prime iff 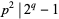 . Therefore, Mersenne primes are not Wieferich primes.
. Therefore, Mersenne primes are not Wieferich primes.
REFERENCES:
Bateman, P. T.; Selfridge, J. L.; and Wagstaff, S. S. "The New Mersenne Conjecture." Amer. Math. Monthly 96, 125-128, 1989.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 66, 1987.
Beiler, A. H. Ch. 3 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.
Bell, E. T. Mathematics: Queen and Servant of Science. Washington, DC: Math. Assoc. Amer., 1987.
Caldwell, C. "Mersenne Primes: History, Theorems and Lists." http://www.utm.edu/research/primes/mersenne/.
Caldwell, C. K. "The Top Twenty: Mersenne Primes." http://www.utm.edu/research/primes/lists/top20/Mersenne.html.
Caldwell, C. "Where Is the Next Mersenne Prime?" http://primes.utm.edu/notes/faq/NextMersenne.html.
Colquitt, W. N. and Welsh, L. Jr. "A New Mersenne Prime." Math. Comput. 56, 867-870, 1991.
Conway, J. H. and Guy, R. K. "Mersenne's Numbers." In The Book of Numbers. New York: Springer-Verlag, pp. 135-137, 1996.
Devlin, K. "World's Largest Prime." FOCUS: Newsletter Math. Assoc. Amer. 17, 1, Dec. 1997.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 13, 2005.
Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 47-51, 2000.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 85, 1984.
Gardner, M. "Patterns in Primes Are a Clue to the Strong Law of Small Numbers." Sci. Amer. 243, 18-28, Dec. 1980.
Gillies, D. B. "Three New Mersenne Primes and a Statistical Theory." Math Comput. 18, 93-97, 1964.
GIMPS. "GIMPS Milestones Report." http://v5www.mersenne.org/report_milestones/.
Great Internet Prime Search: GIMPS. Finding World World Primes Since 1996. "List of Known Mersenne Prime Numbers." http://www.mersenne.org/primes/.
Guy, R. K. "Mersenne Primes. Repunits. Fermat Numbers. Primes of Shape 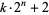 [sic]." §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 8-13, 1994.
[sic]." §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 8-13, 1994.
Haghighi, M. "Computation of Mersenne Primes Using a Cray X-MP." Intl. J. Comput. Math. 41, 251-259, 1992.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 14-16, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.
Kraitchik, M. "Mersenne Numbers and Perfect Numbers." §3.5 in Mathematical Recreations. New York: W. W. Norton, pp. 70-73, 1942.
Kravitz, S. and Berg, M. "Lucas' Test for Mersenne Numbers 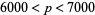 ." Math. Comput. 18, 148-149, 1964.
." Math. Comput. 18, 148-149, 1964.
Lehmer, D. H. "On Lucas's Test for the Primality of Mersenne's Numbers." J. London Math. Soc. 10, 162-165, 1935.
Leyland, P. http://research.microsoft.com/~pleyland/factorization/factors/mersenne.txt.
Mersenne, M. Cogitata Physico-Mathematica. 1644.
Noll, C. and Nickel, L. "The 25th and 26th Mersenne Primes." Math. Comput. 35, 1387-1390, 1980.
Powers, R. E. "The Tenth Perfect Number." Amer. Math. Monthly 18, 195-196, 1911.
Powers, R. E. "Note on a Mersenne Number." Bull. Amer. Math. Soc. 40, 883, 1934.
Robinson, R. M. "Mersenne and Fermat Numbers." Proc. Amer. Math. Soc. 5, 842-846, 1954.
Shankland, S. "Cooperative Computing Finds Top Prime Number." ZDNet News: Hardware. Dec. 2, 2003. http://zdnet.com.com/2100-1103_2-5112827.html?tag=zdfd.newsfeed.
Sloane, N. J. A. Sequences A000043/M0672 and A000668/M2696 in "The On-Line Encyclopedia of Integer Sequences."
Slowinski, D. "Searching for the 27th Mersenne Prime." J. Recreat. Math. 11, 258-261, 1978-1979.
Tuckerman, B. "The 24th Mersenne Prime." Proc. Nat. Acad. Sci. USA 68, 2319-2320, 1971.
Uhler, H. S. "A Brief History of the Investigations on Mersenne Numbers and the Latest Immense Primes." Scripta Math. 18, 122-131, 1952.
Uspensky, J. V. and Heaslet, M. A. Elementary Number Theory. New York: McGraw-Hill, 1939.
Welsh, L. "Marin Mersenne." http://www.utm.edu/research/primes/mersenne/LukeMirror/mersenne.htm.
Welsh, L. "Mersenne Numbers & Mersenne Primes Bibliography." http://www.utm.edu/research/primes/mersenne/LukeMirror/biblio.htm.
Whitehouse, D. "Number Takes Prime Position." December 5, 2001. BBC News online. http://news.bbc.co.uk/hi/english/sci/tech/newsid_1693000/1693364.stm.
Woltman, G. "The GREAT Internet Mersenne Prime Search." http://www.mersenne.org/prime.htm.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|