The Eulerian number  gives the number of permutations of {1,2,...,n}" src="https://mathworld.wolfram.com/images/equations/EulerianNumber/Inline2.gif" style="height:15px; width:69px" /> having 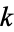 permutation ascents (Graham et al. 1994, p. 267). Note that a slightly different definition of Eulerian number is used by Comtet (1974), who defines the Eulerian number  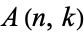(sometimes also denoted 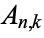) as the number of permutation runs of length 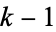, and hence .

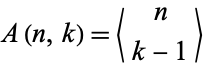The Eulerian numbers are given explicitly by the sum

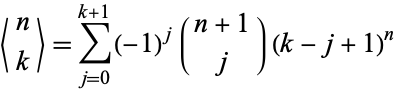(1)

(Comtet 1974, p.  243). The Eulerian numbers satisfy the sum identity

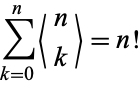(2)

as well as Worpitzky's identity

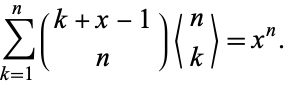(3)

Eulerian numbers also arise in the surprising context of integrating the sinc function, and also in sums of the form

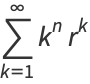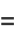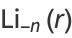			(4)
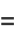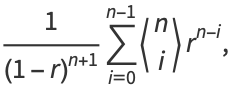			(5)

where 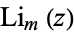 is the polylogarithm function.  is therefore given by the coefficient of 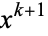 in

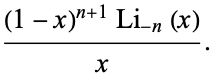(6)

 has the exponential generating function

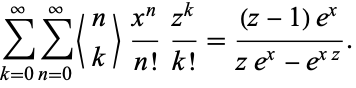(7)

The Eulerian numbers 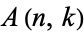 satisfy the recurrence relation

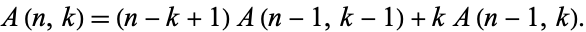(8)

Special cases are given by

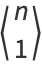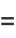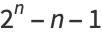			(9)
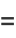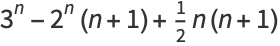			(10)
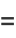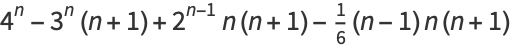			(11)

and summarized in the following table.

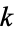	OEIS	, , , ...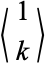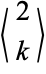
1	A000295	0, 1, 4, 11, 26, 57, 120, 247, 502, 1013, ...
2	A000460	0, 0, 1, 11, 66, 302, 1191, 4293, 14608, ...
3	A000498	0, 0, 0, 1, 26, 302, 2416, 15619, 88234, ...

The arrangement of the numbers 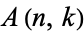 into a triangle gives Euler's number triangle

(12)

(OEIS A008292). Therefore, the Eulerian numbers represent a sort of generalization of the binomial coefficients where the defining recurrence relation weights the sum of neighbors by their row and column numbers, respectively.

REFERENCES:

Abramson, M. and Moser, W. O. J. "Permutations without Rising or Falling 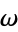-Sequences." Ann. Math. Statist. 38, 1245-1254, 1967.

André, D. "Mémoir sur les couples actifs de permutations." Mem. della Pontificia Acad. Romana dei Nuovo Lincei 23, 189-223, 1906.

Carlitz, L. "Note on a Paper of Shanks." Amer. Math. Monthly 59, 239-241, 1952.

Carlitz, L. "Eulerian Numbers and Polynomials." Math. Mag. 32, 247-260, 1959.

Carlitz, L. "Eulerian Numbers and Polynomials of Higher Order." Duke Math. J. 27, 401-423, 1960.

Carlitz, L. "A Note on the Eulerian Numbers." Arch. Math. 14, 383-390, 1963.

Carlitz, L. and Riordan, J. "Congruences for Eulerian Numbers." Duke Math. J. 20, 339-343, 1953.

Carlitz, L.; Roselle, D. P.; and Scoville, R. "Permutations and Sequences with Repetitions by Number of Increase." J. Combin. Th. 1, 350-374, 1966.

Cesàro, E. "Dérivées des fonctions de fonctions." Nouv. Ann. 5, 305-327, 1886.

Comtet, L. "Permutations by Number of Rises; Eulerian Numbers." §6.5 in Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, pp. 51 and 240-246, 1974.

David, F. N.; Kendall, M. G.; and Barton, D. E. Symmetric Function and Allied Tables. Cambridge, England: Cambridge University Press, p. 260, 1966.

Dillon, J. F.; Roselle, D. P. "Eulerian Numbers of Higher Order." Duke Math. J. 35, 247-256, 1968.

Foata, D. and Schützenberger, M.-P. Théorie géométrique des polynômes Eulériens. Berlin: Springer-Verlag, 1970.

Frobenius, F. G. "Ueber die Bernoullischen Zahlen und die Eulerischen Polynome." Sitzungsber. Preuss. Akad. Wiss., pp. 808-847, 1910.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Eulerian Numbers." §6.2 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 267-272, 1994.

Kimber, A. C. "Eulerian Numbers." Supplement to Encyclopedia of Statistical Sciences. (Ed. S. Kotz, N. L. Johnson, and C. B. Read). New York: Wiley, pp. 59-60, 1989.

Poussin, F. "Sur une propriété arithmétique de certains polynomes associés aux nombres d'Euler." C. R. Acad. Sci. Paris Sér. A-B 266, A392-A393, 1968.

Salama, I. A. and Kupper, L. L. "A Geometric Interpretation for the Eulerian Numbers." Amer. Math. Monthly 93, 51-52, 1986.

Schrutka, L. "Eine neue Einleitung der Permutationen." Math. Ann. 118, 246-250, 1941.

Shanks, E. B. "Iterated Sums of Powers of the Binomial Coefficients." Amer. Math. Monthly 58, 404-407, 1951.

Sloane, N. J. A. Sequences A000295/M3416, A000460/M4795, A000498/M5188, and A008292 in "The On-Line Encyclopedia of Integer Sequences."

Tomić, M. "Sur une nouvelle classe de polynômes de la théorie des fonctions spéciales." Publ. Fac. Elect. U. Belgrade, No. 38, 1960.

Toscano, L. "Su due sviluppi della potenza di un binomio, 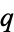-coefficienti di Eulero." Bull. S. M. Calabrese 16, 1-8, 1965.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الفكرية يطلق باقة من النشاطات الرقمية الخاصة بشهر المحرم

العتبة العباسية المقدسة تختتم السلسلة الأولى لمشروع المحاضرات القرآنية العاشورائية في بابل

العتبة العباسية المقدسة تسلّم راية العزاء إلى تجمّع مواكب محافظة الديوانية

قسم الشؤون الفكرية يواصل إقامة المجالس الحسينية ضمن سلسلة (بيوت النعيم)

المزيد

الآخبار الصحية

لكبح الجوع وخسارة الوزن.. "سر بسيط" في نظام جوكوفيتش ؟

هل يساعد الرجيم في علاج الأمراض العقلية؟

لحماية أسنان طفلك.. هذا الفيتامين يقلل خطر التسوس

أكل الطعام بسرعة.. طريق سريع إلى أمراض خطيرة

المزيد

الآخبار التكنلوجية

ما هي أفضل درجة حرارة لتكييف الهواء في السيارة؟

ذوبان الأنهار الجليدية يوقظ "عمالقة نائمة"!

9 يوليو يشهد أقصر يوم في التاريخ المسجل ؟!!

راتبه عشرات ملايين الدولارات.. زوكربرغ يخطف "عقل أبل"

المزيد