A double Mersenne number is a number of the form

where 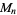 is a Mersenne number. The first few double Mersenne numbers are 1, 7, 127, 32767, 2147483647, 9223372036854775807, ... (OEIS A077585).

A double Mersenne number that is prime is called a double Mersenne prime. Since a Mersenne prime 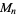 can be prime only for prime 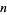, a double Mersenne prime can be prime only for prime 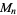, i.e.,  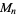a Mersenne prime. Double Mersenne numbers are prime for 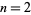, 3, 5, 7, corresponding to the sequence 7, 127, 2147483647, 170141183460469231731687303715884105727, ... (OEIS A077586).

The next four 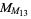, , 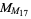, 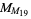and 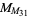 have known factors summarized in the following table. The status of all other double Mersenne numbers is unknown, with  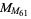being the smallest unresolved case. Since this number has 694127911065419642 digits, it is much too large for the usual Lucas-Lehmer test to be practical. The only possible method of determining the status of this number is therefore attempting to find small divisors (or discovery of an efficient primality test for this type of number). T. Forbes has organized a distributed search, but thus no factors have been found although about 80% of the trial divisors up to  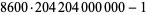have been checked. Edgington maintains a list of known factorizations of double Mersenne numbers.

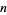	factors	reference
13	338193759479, C2455	Wilfrid Keller (1976)
17	231733529	Raphael Robinson (1957)
19	62914441	Raphael Robinson (1957)
31	295257526626031	Guy Haworth (1983, 1987)
	87054709261955177	Keller (1994)
	242557615644693265201	Keiser and Forbes (1999)
	178021379228511215367151	Mayer (2005)

REFERENCES:

Edgington, W. "Will Edgington's Mersenne Page." https://www.garlic.com/~wedgingt/mersenne.html.

Edgington, W. "Status of M(M(p)) where M(p) is a Mersenne Prime." https://anthony.d.forbes.googlepages.com/mm61prog.htm.

Forbes, T. "MM61: A Search for a Factor of 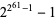." https://anthony.d.forbes.googlepages.com/mm61.htm.

Forbes, T. "MM61: A Search for a Factor of 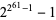. Progress: 2 March 2004." https://www.ltkz.demon.co.uk/ar2/mm61prog.htm.

Haworth, G. M. Notes on Mersenne Numbers. Privately produced manuscript, 1987.

Mayer, E. W. "Fourth Known Factor of M(M31)." 21 Jun 2005. https://listserv.nodak.edu/cgi-bin/wa.exe?A2=ind0506&L=nmbrthry&T=0&F=&S=&P=2514.

Sloane, N. J. A. Sequences A077585 and A077586 in "The On-Line Encyclopedia of Integer Sequences."

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد