Sequences
المؤلف:
Sloane, N. J. A.
المصدر:
Sequences A070864, A070867, A070868, and A070885 in "The On-Line Encyclopedia of Integer Sequences."
الجزء والصفحة:
...
8-11-2020
1968
Sequences
Wolfram (2002, p. 123) considered the sequence related to the Collatz problem obtained by iterating
![w_n=<span style=]() {3/2w_(n-1) for w_(n-1) even; 3/2(w_(n-1)+1) for w_(n-1) odd " src="https://mathworld.wolfram.com/images/equations/WolframSequences/NumberedEquation1.gif" style="height:56px; width:204px" /> |
(1)
|
starting with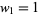 
. This gives the sequence 1, 3, 6, 9, 15, 24, 36, 54, 81, 123, ... (OEIS A070885). The first 40 iterations are illustrated above, with each row being one iteration and the number obtained in that iteration represented in binary.
Another set of sequences are given by
![w_n=<span style=]() {5/2w_(n-1) for w_(n-1) even; 1/2(w_(n-1)+1) for w_(n-1) odd " src="https://mathworld.wolfram.com/images/equations/WolframSequences/NumberedEquation2.gif" style="height:56px; width:204px" /> |
(2)
|
starting with various initial values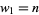 
. Interestingly, while taking 
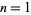, 2, 3, 4, 5, 7, 9, 10, ... give simple periodic sequences, the cases 
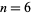, 8, give complicated aperiodic sequences. 100 iterations starting at each of 
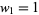to 10 are illustrated above.
Wolfram also considered the sequence 1, 1, 3, 3, 3, 5, 3, ... (OEIS A070864) defined by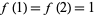 
and
 |
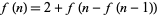(3)
|
(Wolfram 2002, p. 129, (b)), the sequence 1, 1, 2, 2, 2, 4, 3, 4, 4, 4, ... (OEIS A070867) defined by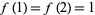 
and
 |
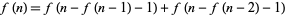(4)
|
(Wolfram 2002, p. 129, (f)), and the sequence 1, 1, 2, 2, 2, 3, 3, 4, 3, 4, ... (OEIS A070868) defined by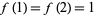 
and
 |
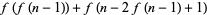(5)
|
(Wolfram 2002, p. 129, (h)).
REFERENCES:
Sloane, N. J. A. Sequences A070864, A070867, A070868, and A070885 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 129, 2002.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
