المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Casoratian |
 762
 02:20 صباحاً
date: 24-10-2020 |
Author : Zwillinger, D. (Ed.). 
Book or Source : CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press 
Page and Part : p. 229|
Read More
Date: 23-8-2020
563
Date: 2-12-2020
2136
Date: 28-10-2019
1093
|
The Casoratian of sequences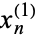 
, 
, ..., 
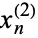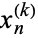is defined by the 
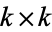determinant
 |
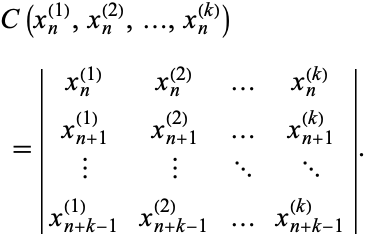The Casoratian is implemented in the Wolfram Language as Casoratian[
y1, y2, ...
, n].
The solutions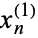 
, 
, ..., 
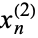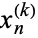of the linear difference equation
 |
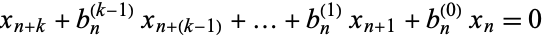for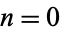 
, 1, ..., are linearly independent sequences iff their Casoratian is nonzero for 
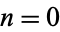(Zwillinger 1995).
REFERENCES:
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 229, 1995.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
