
Nearest Integer Function
 المؤلف:
Graham, R. L.; Knuth, D. E.; and Patashnik, O.
المؤلف:
Graham, R. L.; Knuth, D. E.; and Patashnik, O.
 المصدر:
"Integer Functions." Ch. 3 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley
المصدر:
"Integer Functions." Ch. 3 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley
 الجزء والصفحة:
...
الجزء والصفحة:
...
 21-10-2020
21-10-2020
 2048
2048
Nearest Integer Function
The nearest integer function, also called nint or the round function, is defined such that 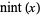 is the integer closest to
is the integer closest to  . While the notation
. While the notation ![|_x]](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline3.gif) is sometimes used to denote the nearest integer function (Hastad et al. 1988), this notation is rather cumbersome and is not recommended. Also note that while
is sometimes used to denote the nearest integer function (Hastad et al. 1988), this notation is rather cumbersome and is not recommended. Also note that while ![[x]](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline4.gif) is sometimes used to denote the nearest integer function,
is sometimes used to denote the nearest integer function, ![[x]](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline5.gif) is also commonly used to denote the floor function
is also commonly used to denote the floor function 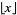 (including by Gauss in his third proof of quadratic reciprocity in 1808), so this notational use is also discouraged.
(including by Gauss in his third proof of quadratic reciprocity in 1808), so this notational use is also discouraged.
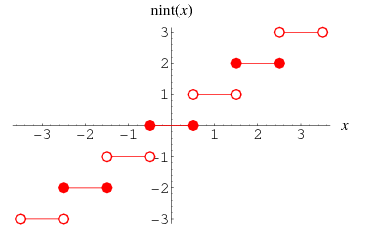
Since the definition is ambiguous for half-integers, the additional rule that half-integers are always rounded to even numbers is usually added in order to avoid statistical biasing. For example, 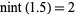 ,
, 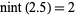 ,
, 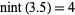 ,
, 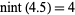 , etc. This convention is followed in the C math.h library function rint, as well as in the Wolfram Language, where the nearest integer function is implemented as Round[x].
, etc. This convention is followed in the C math.h library function rint, as well as in the Wolfram Language, where the nearest integer function is implemented as Round[x].
Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used. Here, S&O indicates Spanier and Oldham (1987).
| notation |
name |
S&O |
Graham et al. |
Wolfram Language |
![[x]](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline11.gif) |
ceiling function |
-- |
ceiling, least integer |
Ceiling[x] |
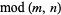 |
congruence |
-- |
-- |
Mod[m, n] |
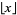 |
floor function |
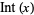 |
floor, greatest integer, integer part |
Floor[x] |
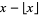 |
fractional value |
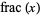 |
fractional part or ![<span style=]() {x}" src="https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline17.gif" style="height:15px; width:17px" /> {x}" src="https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline17.gif" style="height:15px; width:17px" /> |
SawtoothWave[x] |
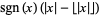 |
fractional part |
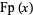 |
no name |
FractionalPart[x] |
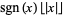 |
integer part |
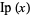 |
no name |
IntegerPart[x] |
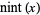 |
nearest integer function |
-- |
-- |
Round[x] |
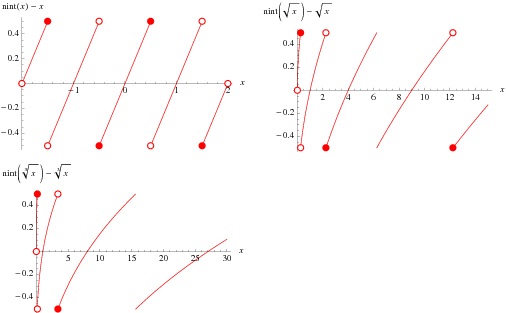
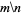 |
quotient |
-- |
-- |
Quotient[m, n] |
The plots above illustrate ![x^(1/n)-[x^(1/n)]](https://mathworld.wolfram.com/images/equations/NearestIntegerFunction/Inline24.gif) for small
for small 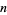 .
.
The nearest integer function can also be extended to the complex plane, as illustrated above.
REFERENCES:
Graham, R. L.; Knuth, D. E.; and Patashnik, O. "Integer Functions." Ch. 3 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, pp. 67-101, 1994.
Hastad, J.; Just, B.; Lagarias, J. C.; and Schnorr, C. P. "Polynomial Time Algorithms for Finding Integer Relations among Real Numbers." SIAM J. Comput. 18, 859-881, 1988.
Spanier, J.; Myland, J.; and Oldham, K. B. An Atlas of Functions, 2nd ed. Washington, DC: Hemisphere, 1987.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


