The set {infty}" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline1.gif" style="height:15px; width:50px" />, obtained by adjoining one improper element to the set 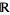 of real numbers, is the set of projectively extended real numbers. Although notation is not completely standardized,  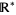is used here to denote this set of extended real numbers. 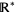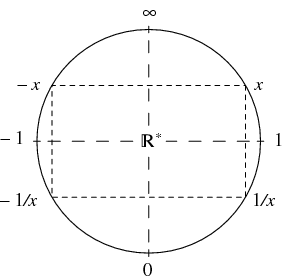With an appropriate topology,  is the one-point compactification (or projective closure) of 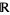. As shown above, the cross section of the Riemann sphere consisting of its "real axis" and "north pole" can be used to visualize 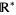. The improper element, projective infinity (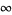), then corresponds with the ideal point, the "north pole."

In contrast to the signed affine infinities (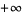 and 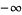) of the affinely extended real numbers 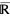, projective infinity, 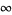, is unsigned, like 0. Regrettably,  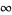is also unordered, i.e., for  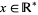it can be said neither that  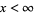nor that 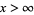. For this reason,  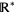is used much less often in real analysis than is 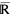. Thus, if context is not specified, "the extended real numbers" normally refers to 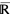, not .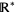

Arithmetic operations can be partially extended from 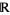 to ,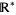

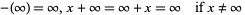	(1)
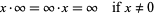	(2)
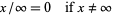	(3)
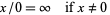	(4)

(by contrast, 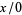 is undefined in 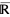). The expressions  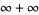and 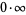 are most often left undefined in .

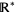The exponential function 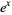 cannot be extended to 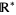. On the other hand,  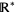is useful when dealing with rational functions and certain other functions. For example, if  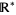is used as the range of 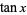, then by taking  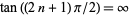for integer 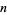, the domain of the function can be extended to all of .

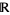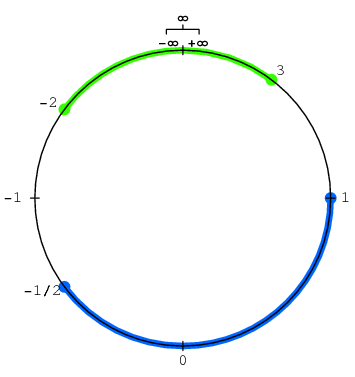
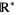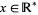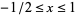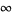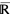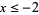The above figure shows two intervals on . One of them is the set of  such that , and of course it can be written conveniently using ordinary interval notation, as . But the other interval consisting of  (which may be thought of as a "merger" of the two signed infinities of the affine extension, ) together with all reals  such that either  or 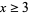, cannot be indicated so conveniently using ordinary notation.

This might not be of much interest except for the fact that such intervals arise in those systems of interval arithmetic that allow division by intervals containing 0. As an example, consider . This division can be performed in the Wolfram Language using Interval[{" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline49.gif" style="height:15px; width:5px" />6,7}" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline50.gif" style="height:15px; width:5px" />]/Interval[{" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline51.gif" style="height:15px; width:5px" />-3,2}" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline52.gif" style="height:15px; width:5px" />], which yields Interval[{" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline53.gif" style="height:15px; width:5px" />-Infinity, -2}" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline54.gif" style="height:15px; width:5px" />, {" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline55.gif" style="height:15px; width:5px" />3, Infinity}" src="https://mathworld.wolfram.com/images/equations/ProjectivelyExtendedRealNumbers/Inline56.gif" style="height:15px; width:5px" />]. This represents , the union of two intervals in the affine extension. But, as the figure above indicates, the corresponding set in the projective extension is a single interval, and it would be nice to be able to denote it as such. Various conventions have been suggested for denoting such intervals. According to one convention (Reinsch 1982, pp. 88-89), on the number circle representing 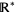, let  denote the closed interval that is traced going in a counterclockwise direction from 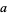 to 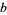. According to this definition, for example,  retains its former meaning. But the definition also applies even when 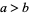, allowing the answer to the interval division above to be written concisely as .

REFERENCES:

Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia," Vol. 3. Dordrecht, Netherlands: Reidel, p. 193, 1988.

Reinsch, C. "A Synopsis of Interval Arithmetic for the Designer of Programming Languages." In The Relationship Between Numerical Computation and Programming Languages (Ed. J. K. Reid). Amsterdam, Netherlands: North-Holland, pp. 85-97, 1982.

اخر الاخبار

اخبار العتبة العباسية المقدسة

وفد العتبة العباسية المقدسة يجري جولة في أروقة معرض بغداد الدولي للكتاب

شعبة التوجيه الديني النسوي تطلق برنامجًا قرآنيًّا لزائرات مرقد أبي الفضل العباس (عليه السلام)

جامعة الكفيل تطلق دورة تدريبية عن تقييم الأداء الجامعي لعدد من ملاكاتها

المجمع العلمي يقيم محفلًا قرآنيًا بذكرى ولادة الصادقين (صلوات الله عليهما)

المزيد

الآخبار الصحية

هل يتنبأ الذكاء الاصطناعي بأمراضنا قبل حدوثها؟

وداعا للنظارات.. قطرة عين واحدة قد تغير كل شيء ؟

دراسة تكشف تأثير "تيك توك" وتطبيقات الفيديو على سلوك الأطفال

"أسرار خفية" في الشاي الأخضر.. تغير قواعد الصحة والوزن

المزيد

الآخبار التكنلوجية

أول قطار يعمل بالهيدروجين في أميركا يدخل الخدمة رسميًا

أجهزة أبل القادمة.. "حصن منيع" في عصر الهجمات الرقمية !

روسيا: تطلق قمرين اصطناعيين بواسطة الصاروخ سويوز 2.1

ميزة ثورية.. أبل تدخل عالم قياس ضغط الدم

المزيد