p-adic Number
A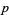 
-adic number is an extension of the field of rationals such that congruences modulo powers of a fixed prime 
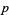are related to proximity in the so called "
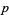-adic metric."
Any nonzero rational number 
can be represented by
 |
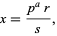(1)
|
where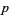 
is a prime number, 
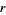and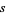 
are integers not divisible by 
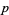, and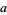 
is a unique integer. Then define the p-adic norm of 
by
 |
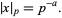(2)
|
Also define the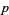 
-adic norm
 |
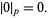(3)
|
The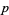 
-adics were probably first introduced by Hensel (1897) in a paper which was concerned with the development of algebraic numbers in power series. 
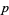-adic numbers were then generalized to valuations by Kűrschák in 1913. Hasse (1923) subsequently formulated the Hasse principle, which is one of the chief applications of local field theory. Skolem's 
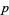-adic method, which is used in attacking certain Diophantine equations, is another powerful application of 
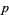-adic numbers. Another application is the theorem that the harmonic numbers 
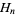are never integers (except for 
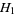). A similar application is the proof of the von Staudt-Clausen theorem using the 
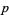-adic valuation, although the technical details are somewhat difficult. Yet another application is provided by the Mahler-Lech theorem.
Every rational 
has an "essentially" unique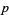 
-adic expansion ("essentially" since zero terms can always be added at the beginning)
 |
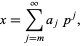(4)
|
with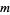 
an integer, 
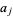the integers between 0 and 
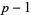inclusive, and where the sum is convergent with respect to 
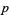-adic valuation. If 
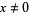and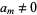 
, then the expansion is unique. Burger and Struppeck (1996) show that for 
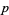a prime and 
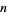a positive integer,
 |
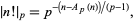(5)
|
where the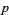 
-adic expansion of 
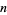is
 |
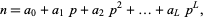(6)
|
and
 |
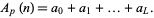(7)
|
For sufficiently large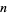 
,
 |
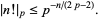(8)
|
The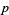 
-adic valuation on 
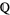gives rise to the 
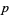-adic metric
 |
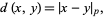(9)
|
which in turn gives rise to the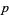 
-adic topology. It can be shown that the rationals, together with the 
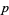-adic metric, do not form a complete metric space. The completion of this space can therefore be constructed, and the set of 
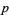-adic numbers 
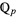is defined to be this completed space.
Just as the real numbers are the completion of the rationals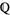 
with respect to the usual absolute valuation 
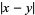, the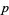 
-adic numbers are the completion of 
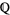with respect to the 
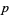-adic valuation 
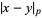. The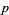 
-adic numbers are useful in solving Diophantine equations. For example, the equation 
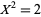can easily be shown to have no solutions in the field of 2-adic numbers (we simply take the valuation of both sides). Because the 2-adic numbers contain the rationals as a subset, we can immediately see that the equation has no solutions in the rationals. So we have an immediate proof of the irrationality of 
.
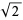This is a common argument that is used in solving these types of equations: in order to show that an equation has no solutions in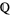 
, we show that it has no solutions in an extension field. For another example, consider 
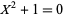. This equation has no solutions in 
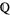because it has no solutions in the reals 
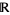, and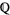 
is a subset of 
.
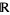Now consider the converse. Suppose we have an equation that does have solutions in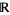 
and in all the 
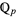for every prime 
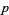. Can we conclude that the equation has a solution in 
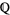? Unfortunately, in general, the answer is no, but there are classes of equations for which the answer is yes. Such equations are said to satisfy the Hasse principle.
REFERENCES:
Burger, E. B. and Struppeck, T. "Does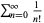 
Really Converge? Infinite Series and p-adic Analysis." Amer. Math. Monthly 103, 565-577, 1996.
Cassels, J. W. S. Ch. 2 in Lectures on Elliptic Curves. New York: Cambridge University Press, 1991.
Cassels, J. W. S. and Scott, J. W. Local Fields. Cambridge, England: Cambridge University Press, 1986.
De Smedt, S. "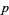
-adic Arithmetic." The Mathematica J. 9, 349-357, 2004.
Gouvêa, F. Q. P-adic Numbers: An Introduction, 2nd ed. New York: Springer-Verlag, 1997.
Hasse, H. "Über die Darstellbarkeit von Zahlen durch quadratische Formen im Körper der rationalen Zahlen." J. reine angew. Math. 152, 129-148, 1923.
Hasse, H. "Die Normenresttheorie relativ-Abelscher Zahlkörper als Klassenkörpertheorie in Kleinen." J. reine angew. Math. 162, 145-154, 1930.
Hensel, K. "Über eine neue Begründung der Theorie der algebraischen Zahlen." Jahresber. Deutsch. Math. Verein 6, 83-88, 1897.
Kakol, J.; De Grande-De Kimpe, N.; and Perez-Garcia, C. (Eds.). p-adic Functional Analysis. New York: Dekker, 1999.
Koblitz, N. P-adic Numbers, P-adic Analysis, and Zeta-Functions, 2nd ed. New York: Springer-Verlag, 1984.
Koch, H. "Valuations." Ch. 4 in Number Theory: Algebraic Numbers and Functions. Providence, RI: Amer. Math. Soc., pp. 103-139, 2000.
Mahler, K. P-adic Numbers and Their Functions, 2nd ed. Cambridge, England: Cambridge University Press, 1981.
Ostrowski, A. "Über sogennante perfekte Körper." J. reine angew. Math. 147, 191-204, 1917.
Vladimirov, V. S. "Tables of Integrals of Complex-Valued Functions of p.-adic Arguments" 22 Nov 1999. https://arxiv.org/abs/math-ph/9911027.
Weisstein, E. W. "Books about P-adic Numbers." https://www.ericweisstein.com/encyclopedias/books/P-adicNumbers.html.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
