Pell Number

The Pell numbers are the numbers obtained by the 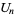s in the Lucas sequence with  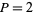and 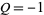. They correspond to the Pell polynomial 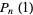. Similarly, the Pell-Lucas numbers are the 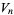s in the Lucas sequence with  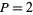and 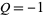, and correspond to the Pell-Lucas polynomial .

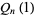The Pell numbers and Pell-Lucas numbers are also equal to

			(1)
			(2)

where 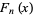 is a Fibonacci polynomial.

The Pell and Pell-Lucas numbers satisfy the recurrence relation

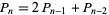(3)

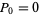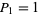with initial conditions  and  for the Pell numbers and  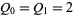for the Pell-Lucas numbers.

The 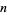th Pell and Pell-Lucas numbers are explicitly given by the Binet-type formulas

			(4)
			(5)

The 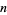th Pell and Pell-Lucas numbers are given by the binomial sums

			(6)
			(7)

respectively.

The Pell and Pell-Lucas numbers satisfy the identities

			(8)
			(9)
			(10)

and

			(11)
			(12)

For 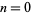, 1, ..., the Pell numbers are 0, 1, 2, 5, 12, 29, 70, 169, 408, 985, 2378, ... (OEIS A000129).

For a Pell number 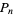 to be prime, it is necessary that  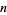be prime. The indices of (probable) prime Pell numbers are 2, 3, 5, 11, 13, 29, 41, 53, 59, 89, 97, 101, 167, 181, 191, 523, 929, 1217, 1301, 1361, 2087, 2273, 2393, 8093, 13339, 14033, 23747, 28183, 34429, 36749, 90197, ... (OEIS A096650), with no others less than  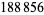(E. W. Weisstein, Mar. 21, 2009). The largest proven prime has index 13339 and 5106 digits (https://primes.utm.edu/primes/page.php?id=24572), whereas the largest known probable prime has index 90197 and 34525 digits (T. D. Noe, Sep. 2004).

For 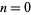, 1, ..., the Pell-Lucas numbers are 2, 2, 6, 14, 34, 82, 198, 478, 1154, 2786, 6726, ... (OEIS A002203). As can be seen, they are always even.

For a Pell-Lucas number 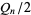 to be prime, it is necessary that  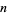be either prime or a power of 2. The indices of  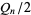that are (probable) primes are 2, 3, 4, 5, 7, 8, 16, 19, 29, 47, 59, 163, 257, 421, 937, 947, 1493, 1901, 6689, 8087, 9679, 28753, 79043, 129127, 145969, 165799, 168677, 170413, 172243, ... (OEIS A099088). The following table summarizes the largest known Pell-Lucas primes.

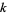	decimal digits	discoverer	date
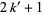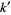		E. W. Weisstein	May 19, 2006
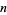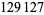		E. W. Weisstein	Aug. 29, 2006
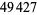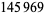		E. W. Weisstein	Nov. 16, 2006
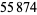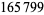		E. W. Weisstein	Nov. 26, 2006
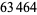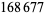		E. W. Weisstein	Dec. 10, 2006
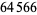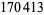		E. W. Weisstein	Jan. 15, 2007

There are no others for 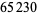 (E. W. Weisstein, Mar. 21, 2009). The largest proven prime has index 9679 and 3705 decimal digits (https://primes.utm.edu/primes/page.php?id=27783). These indices  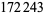are a superset via  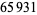of the indices  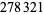of prime NSW numbers.

The only triangular Pell number is 1 (McDaniel 1996).

REFERENCES:

McDaniel, W. L. "Triangular Numbers in the Pell Sequence." Fib. Quart. 34, 105-107, 1996.

Ram, R. "Pell Numbers Formulae." https://users.tellurian.net/hsejar/maths/pell/.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 53-57, 1996.

Sloane, N. J. A. Sequences A000129/M1413, A002203/M0360, A096650, and A099088 in "The On-Line Encyclopedia of Integer Sequences."