| sequence |
OEIS |
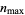 |
digits |
discoverer |
search limit |
comments |
| alternating factorial |
A001272 |
59961 |
260448 |
M. Rodenkirch (Sep. 18, 2017) |
100000 (M. Rodenkirch, Dec. 15, 2017) |
finite sequence; largest certified prime has index 661; the rest are probable primes |
| Apéry-constant prime |
A119334 |
141 |
141 |
E. W. Weisstein (May 14, 2006) |
9089 (E. W. Weisstein, Mar. 22, 2008) |
status unknown |
Apéry number 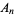 |
A092825 |
6624 |
10136 |
E. W. Weisstein (Mar. 2004) |
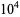 (E. W. Weisstein, Mar. 2004) (E. W. Weisstein, Mar. 2004) |
probable prime |
Apéry number 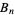 |
|
8 |
7 |
E. W. Weisstein (Mar. 2004) |
1103800 (E. W. Weisstein, Mar. 16, 2004) |
proven prime (trivial) |
| Bell number |
A051130 |
2841 |
6539 |
|
30447 (E. W. Weisstein, Apr. 23, 2006) |
proven prime by I. L. Canestro in 2004 |
| Belphegor prime |
A232448 |
181298 |
362601 |
S. Batalov (Nov. 15, 2014) |
? |
status unknown |
Bernoulli number 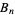 numerator numerator |
A092132 |
42 |
22 |
E. W. Weisstein (Mar. 2004) |
101114 (E. W. Weisstein, Mar. 21, 2009) |
proven prime |
| Catalan-constant prime |
A118328 |
25477 |
25477 |
E. W. Weisstein (May. 5, 2006) |
166896 (E. W. Weisstein, Feb. 8, 2016) |
proven prime (trivial) |
Catalan-Mersenne number 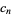 |
|
4 |
39 |
Catalan (1876) |
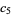 has no prime factor less than has no prime factor less than 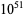 |
Noll; private correspondence with C. K. Caldwell, Aug. 10, 2003; proven prime |
central trinomial coefficient 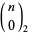 |
|
4 |
2 |
J. Vos Post (Feb. 2005) |
203661 (E. W. Weisstein, Oct. 30, 2015) |
proven prime (trivial) |
central trinomial coefficient cousin 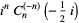 |
A112874 |
31877 |
11139 |
E. W. Weisstein (Feb. 25, 2005) |
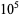 (E. W. Weisstein, Mar. 7, 2005) (E. W. Weisstein, Mar. 7, 2005) |
status unknown |
| Champernowne-constant prime |
A071620 |
37735 |
37735 |
E. W. Weisstein (Jul. 15, 2013) |
105867 (E. W. Weisstein, Oct. 9, 2015) |
status unknown |
| complementary Bell number |
A118018 |
723 |
1266 |
E. W. Weisstein (Apr. 10, 2006) |
32460 (E. W. Weisstein, Aug. 30, 2006) |
proven prime |
| consecutive number sequences of cubic numbers |
|
- |
- |
|
31152 (E. W. Weisstein, Oct. 9, 2015) |
none known |
| consecutive number sequences of Fibonacci numbers |
|
4 |
4 |
|
1891 (E. Weisstein, Jul. 28, 2016) |
proven prime (trivial) |
| consecutive number sequences of odd numbers |
A046036 |
2570 |
9725 |
|
37369 (E. W. Weisstein, Oct. 9, 2015) |
probable prime |
| consecutive number sequences of square numbers |
|
3 |
3 |
|
33432 (E. W. Weisstein, Oct. 9, 2015) |
none known |
| consecutive number sequences of triangular numbers |
|
6 |
9 |
|
35177 (E. W. Weisstein, Oct. 9, 2015) |
proven prime (trivial) |
| consecutive number sequences of reverse integers |
A176024 |
37765 |
177719 |
E. W. Weisstein (Apr. 6, 2010) |
46530 (E. W. Weisstein, Oct. 9, 2015) |
probable prime |
| Copeland-Erdős-constant prime |
A227530 |
292447 |
292447 |
M. Rodenkirch (Dec. 11, 2015) |
500000 (M. Rodenkirch, Jun. 18, 2016) |
probable prime |
Cullen number 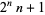 |
A005849 |
6679881 |
2010852 |
PrimeGrid (Aug. 4, 2009) |
13705481 (PrimeGrid, Nov. 19, 2015) |
proven prime (http://primes.utm.edu/top20/page.php?id=6#records) |
Delannoy number 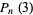 |
|
8 |
6 |
E. W. Weisstein (Mar. 2004) |
7834059 (E. W. Weisstein, Feb. 28, 2006) |
proven prime (trivial) |
double factorial prime 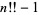 |
A007749 |
145706 |
344538 |
S. Fukui (Apr. 21, 2015) |
? |
? |
double factorial prime 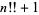 |
A080778 |
123998 |
288864 |
S. Fukui (Jun. 5, 2015) |
? |
? |
double Mersenne number 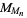 |
|
7 |
39 |
|
60 (G. Haworth 1983) |
proven prime; status of 61 is unknown, search being coordinated by T. Forbes |
| e-prime |
A064118 |
155025 |
155025 |
E. W. Weisstein (Oct. 11, 2010) |
197760 (E. W. Weisstein, Feb. 8, 2016) |
proven prime |
| Euler-Mascheroni-constant prime |
A065815 |
179849 |
179849 |
E. W. Weisstein (Jun. 1, 2011) |
206078 (E. W. Weisstein, Feb. 8, 2016) |
probable prime |
Euler number prime 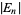 |
A103234 |
510 |
1062 |
|
69574 (S. Plouffe, Aug. 21, 2020) |
proven prime (http://primes.utm.edu/primes/page.php?id=54561) |
| Euler prime |
A005846 |
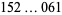 |
398204 |
D. Broadhurst (Feb. 11, 2014) |
? |
proven prime (http://primes.utm.edu/primes/page.php?id=111195) |
factorial prime 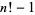 |
A002982 |
208003 |
1015843 |
S. Fukui (Jul. 25, 2016) |
208003 (S. Fukui, Jul. 25, 2016) |
proven prime (http://primes.utm.edu/primes/page.php?id=121944) |
factorial prime 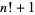 |
A002981 |
150209 |
712354 |
PrimeGrid (Oct. 16, 2013) |
203550 (PrimeGrid, Jul. 25, 2016) |
prime proof underway (http://primes.utm.edu/primes/page.php?id=100445) |
factorial sum 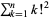 |
A100289 |
32841 |
268128 |
S. Balatov (Jul. 29, 2017) |
? |
probable prime; sequence must be finite |
factorial sum 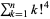 |
|
2 |
2 |
E. W. Weisstein (Jul 16, 2017) |
complete |
proven prime |
factorial sum 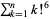 |
A289946 |
102 |
972 |
E. W. Weisstein (Jul 16, 2017) |
complete |
probable prime |
factorial sum 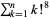 |
|
2 |
3 |
E. W. Weisstein (Jul 16, 2017) |
complete |
finite sequence; all terms proven prime |
factorial sum 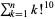 |
|
25 |
252 |
E. W. Weisstein (Jul 16, 2017) |
complete |
finite sequence; all terms proven prime |
Fermat prime 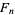 |
|
4 |
5 |
|
32 |
finite sequence; all terms proven prime (trivial) |
Fibonacci prime 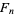 |
A001605 |
3244369 |
678033 |
H. Lifchitz (Nov. 2017) |
? |
probable prime; the largest proven prime has index 104911 (http://primes.utm.edu/top20/page.php?id=39#records) |
fibonorial prime 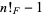 |
A059709 |
15 |
20 |
R. G. Wilson (Feb. 7, 2001) |
800 (E. W. Weisstein, Dec. 8, 2009) |
proven prime (trivial) |
fibonorial prime 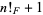 |
A053408 |
28 |
276 |
R. G. Wilson (Jan. 8, 2000) |
800 (E. W. Weisstein, Dec. 8, 2009) |
proven prime (trivial) |
| Glaisher-constant prime |
A118420 |
19692 |
19692 |
E. W. Weisstein (Apr. 29, 2006) |
129009 (E. W. Weisstein, Mar. 1, 2011) |
probable prime |
| Golomb-Dickman constant prime |
A174974 |
2508 |
2508 |
E. W. Weisstein (Apr. 3, 2010) |
15000 E. W. Weisstein, Jul. 25, 2013) |
probable prime |
harmonic number 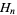 numerator numerator |
A056903 |
81658 |
35479 |
E. W. Weisstein (May 12, 2009) |
81780 (E. W. Weisstein, May 13, 2009) |
status unknown |
| irregular prime |
A000928 |
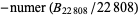 |
71290 |
T. D. Noe (Sep. 28, 2005) |
|
probable prime; largest proven prime is 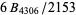 (http://primes.utm.edu/primes/page.php?id=87451) (http://primes.utm.edu/primes/page.php?id=87451) |
| Khinchin-constant prime |
A118327 |
28433 |
28433 |
E. W. Weisstein (Apr. 27, 2006) |
109843 (E. W. Weisstein, Mar. 21, 2009) |
probable prime |
left factorial 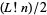 |
A100614 |
12221 |
44640 |
E. W. Weisstein (Oct. 19, 2006) |
12227 (E. W. Weisstein, Oct. 19, 2006) |
status unknown |
Lucas prime 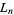 |
A001606 |
1051849 |
219824 |
R. Lifchitz (Mar. 2009) |
|
probable prime; the largest proven prime has index 56003 (http://primes.utm.edu/primes/page.php?id=77992) |
Mersenne prime 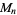 |
A000043 |
82589933 |
24862048 |
GIMPS/P. Laroche/GIMPS (Dec. 7, 2018) |
|
proven prime |
Mills' prime 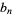 |
A051254 |
13 |
185052 |
S. Batalov (Jul. 19, 2013) |
|
proven prime |
| Motzkin number |
A092831 |
36 |
15 |
E. W. Weisstein (Mar. 2004) |
303228 (E. W. Weisstein, Apr. 2, 2005) |
proven prime |
| natural logarithm of 2-constant prime |
A228226 |
89973 |
89973 |
E. W. Weisstein (Oct. 27, 2015) |
90220 (E. W. Weisstein, Oct. 28, 2015) |
status unknown |
| natural logarithm of 10-constant prime |
A228240 |
75067 |
75067 |
E. W. Weisstein (Oct. 10, 2015) |
77006 (E. W. Weisstein, Oct. 12, 2015) |
status unknown |
near-square prime 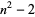 |
A028870 |
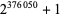 |
226405 |
M. Rodenkirch(Feb. 2016) |
|
status unknown |
near-square prime 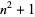 |
A005574 |
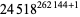 |
1150678 |
S. Scott (Mar. 12, 2008) |
generalized Fermat prime |
proven prime (http://primes.utm.edu/primes/page.php?id=84401) |
near-square prime 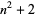 |
A067201 |
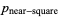 |
110174 |
D. Broadhurst (Apr. 8, 2006) |
|
proven prime (http://primes.utm.edu/primes/page.php?id=77539) |
near-square prime 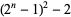 ("Carol" prime) ("Carol" prime) |
A091515 |
653490 |
393441 |
M. Rodenkirch (Jun. 15, 2016) |
? |
status unknown |
near-square prime 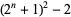 ("Kynea" prime) ("Kynea" prime) |
A091513 |
661478 |
398250 |
M. Rodenkirch (Jun. 19, 2016) |
? |
status unknown |
NSW number 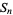 |
A113501 |
86121 |
65931 |
E. W. Weisstein (Jan. 25, 2007) |
subset of Pell-Lucas numbers |
probable prime |
| Padovan sequence number |
A112882 |
727734 |
88874 |
E. W. Weisstein (Apr. 7, 2011) |
729586 (E. W. Weisstein, Apr. 10, 2011) |
status unknown |
| palindromic prime |
A002385 |
 |
474501 |
S. Batalov (Nov. 2014) |
? |
proven prime (http://primes.utm.edu/top20/page.php?id=53#records) |
| partition function P |
A046063 |
1000007396 |
35219 |
E. W. Weisstein (Feb. 12, 2017) |
1000007862 (E. W. Weisstein, Feb. 12, 2017) |
status unknown |
| partition function Q |
A035359 |
81191852 |
? |
M. Alekseyev (Jul. 10, 2015) |
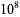 (M. Alekseyev, Jul. 10, 2015) (M. Alekseyev, Jul. 10, 2015) |
status unknown |
Pell number 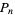 |
A096650 |
90197 |
34525 |
T. D. Noe |
277096 (E. W. Weisstein, Oct. 9, 2015) |
probable prime; largest proven prime has index 13339 and 5106 digits (http://primes.utm.edu/primes/page.php?id=24572) |
Pell-Lucas number 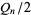 |
A099088 |
172243 |
65931 |
E. W. Weisstein (Jan. 25, 2007) |
270460 (E. W. Weisstein, Oct. 9, 2015) |
probable prime; largest proven prime has index 9679 and 3705 digits (http://primes.utm.edu/primes/page.php?id=27783) |
| Perrin sequence number |
A112881 |
581132 |
70970 |
E. W. Weisstein (Feb. 25, 2011) |
601463 (E. W. Weisstein, Oct. 9, 2015) |
probable prime |
| phi-prime |
A064119 |
97241 |
97241 |
E. W. Weisstein (Jun. 3, 2009) |
500000 (M. Rodenkirch, Jun. 20, 2017) |
status unknown |
| pi-prime |
A060421 |
613373 |
613373 |
A. Bondrescu (May 29, 2016) |
? |
status unknown |
| Pierpont prime |
A005109 |
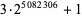 |
1529928 |
A. Brady (Apr. 4, 2009) |
? |
proven prime (http://primes.utm.edu/primes/page.php?id=87449) |
| power difference prime |
A072164 |
7918 |
30870 |
H. Lifchitz (2001) |
|
probable prime |
| primefree sequence inverted primes |
A108156 |
182220 |
38098 |
E. W. Weisstein (Feb. 4, 2006) |
194202 (E. W. Weisstein, May 5, 2006) |
status unknown |
primorial prime 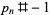 |
A057704 |
85586 |
476310 |
PrimeGrid (Mar. 5, 2012) |
154674 (PrimeGrid, Oct. 30, 2015) |
proven prime |
primorial prime 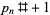 |
A014545 |
33237 |
169966 |
? |
154670 (PrimeGrid, Oct. 30, 2015) |
proven prime (http://primes.utm.edu/primes/page.php?id=21658) |
| Pythagoras-constant prime |
A115377 |
11540 |
11540 |
E. W. Weisstein (Jan. 21, 2005) |
187336 (E. W. Weisstein, Feb. 8, 2016) |
proven prime |
| reflected pi-palindromic prime |
A119351 |
2056 |
4111 |
E. W. Weisstein (May 15, 2006) |
56755 (E. W. Weisstein, Mar. 21, 2009) |
status unknown |
repunit 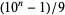 |
A004023 |
270343 |
270343 |
M. Voznyy and A. Budnyy (Jul. 11, 2007) |
|
probable prime; the largest proven prime has index 1031 (http://primes.utm.edu/top20/page.php?id=57) |
| Smarandache prime |
|
- |
- |
- |
344869 (Great Smarandache PRPrime search, Dec. 5, 2016) |
none known |
Smarandache-Wellin prime 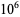 |
A046035 |
1429 |
5719 |
? |
1500000 (M. Rodenkirch, early 2016) |
probable prime |
| Soldner-constant prime |
A122422 |
19474 |
19474 |
E. W. Weisstein (Sep. 6, 2006) |
21757 (E. W. Weisstein, Sep. 7, 2006) |
probable prime |
Sophie Germain prime 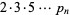 |
A005384 |
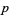 |
388342 |
PrimeGrid (Feb. 29, 2016) |
2559254540925 (PrimeGrid, Feb. 29, 2016) |
proven prime (http://primes.utm.edu/primes/page.php?id=121330) |
| super Catalan number |
A092839 |
216 |
161 |
E. W. Weisstein (Mar. 2004) |
584400 (E. W. Weisstein, Mar. 16, 2004) |
proven prime (trivial) |
| tau function |
A135430 |
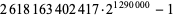 |
555339 |
N. Lygeros and O. Rozier (Sep. 2015) |
? |
probable prime |
| tetradic number |
A068188 |
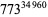 |
180055 |
D. Bedwell (Sep. 8, 2009) |
? |
proven prime (http://primes.utm.edu/top20/page.php?id=53#records) |
| tetranacci number |
A104534 |
155182 |
44228 |
E. W. Weisstein (Oct. 28, 2005) |
236965 (E. W. Weisstein, Mar. 29, 2009) |
probable prime |
Thâbit ibn Kurrah prime 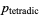 |
A002235 |
11895718 |
3580969 |
PrimeGrid (Jun. 6, 2015) |
12078521 (PrimeGrid, Nov. 3, 2015) |
proven prime (http://primes.utm.edu/primes/page.php?id=120038) |
| Theodorus-constant prime |
A119344 |
170657 |
170657 |
E. W. Weisstein (Aug. 18, 2013) |
193924 (E. W. Weisstein, Feb. 8, 2016) |
status unknown |
| tribonacci number |
A092835 |
96878 |
25639 |
K. Duszenko (Aug. 2003) |
291217 (E. W. Weisstein, Mar. 21, 2009) |
probable prime |
| twin primes |
A001359 |
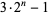 |
388342 |
PrimeGrid (Sep. 14, 2016) |
? |
proven prime (http://primes.utm.edu/top20/page.php?id=1#records) |
| Wagstaff prime |
A000978 |
13372531 |
4025533 |
R. Propper (Sep. 2013) |
? |
probable prime |
| Wall-Sun-Sun prime |
|
- |
- |
|
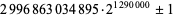 (PrimeGrid, Oct. 30, 2015) (PrimeGrid, Oct. 30, 2015) |
none known |
| Wieferich prime |
A001220 |
3511 |
4 |
|
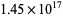 (PrimeGrid, Oct. 30, 2015) (PrimeGrid, Oct. 30, 2015) |
proven prime (trivial) |
| Wilson prime |
A007540 |
563 |
3 |
|
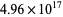 (Costa et al. 2012) (Costa et al. 2012) |
proven prime (trivial) |
| Wolstenholme number |
A111354 |
48590 |
42146 |
T. D. Noe (Mar. 8, 2006) |
|
probable prime |
| Wolstenholme prime |
A088164 |
2124679 |
7 |
|
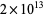 (McIntosh 2004) (McIntosh 2004) |
proven prime (trivial) |
Woodall prime 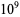 |
A002234 |
17016602 |
5122515 |
D. Bertolotti (Mar. 22, 2018) |
16838832 (PrimeGrid, Mar. 22, 2018) |
proven prime (http://primes.utm.edu/primes/page.php?id=124539) |


