


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-2-2020
Date: 26-6-2020
Date: 1-10-2020
|
If 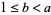 and
and 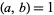 (i.e.,
(i.e., 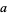 and
and 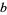 are relatively prime), then
are relatively prime), then 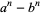 has at least one primitive prime factor with the following two possible exceptions:
has at least one primitive prime factor with the following two possible exceptions:
1. 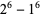 .
.
2. 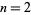 and
and 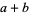 is a power of 2.
is a power of 2.
Similarly, if 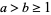 , then
, then 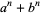 has at least one primitive prime factor with the exception
has at least one primitive prime factor with the exception 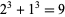 .
.
A specific case of the theorem considers the 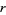 th Mersenne number
th Mersenne number 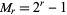 , then each of
, then each of 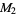 ,
, 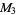 ,
, 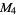 , ... has a prime factor that does not occur as a factor of an earlier member of the sequence, except for
, ... has a prime factor that does not occur as a factor of an earlier member of the sequence, except for 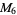 . For example,
. For example, 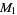 ,
, 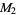 ,
, 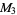 , ... have the factors 3, 7, 5, 31, (1), 127, 17, 73, 11,
, ... have the factors 3, 7, 5, 31, (1), 127, 17, 73, 11, 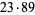 , ... (OEIS A064078) that do not occur in earlier
, ... (OEIS A064078) that do not occur in earlier 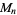 . These factors are sometimes called the Zsigmondy numbers
. These factors are sometimes called the Zsigmondy numbers 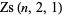 .
.
Zsigmondy's theorem is often useful, especially in group theory, where it is used to prove that various groups have distinct orders except when they are known to be the same (Montgomery 2001).
REFERENCES:
Chabaud, F. and Vaudenay, S. "Links between Differential and Linear Cryptanalysis." EUOROCRYPT 94, pp. 356-365, 1994.
Montgomery, H. "Divisibility of Mersenne Numbers." 17 Sep 2001. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0109&L=nmbrthry&P=1635.
Ribenboim, P. The Little Book of Big Primes. New York: Springer-Verlag, p. 27, 1991.
Sloane, N. J. A. Sequence A064078 in "The On-Line Encyclopedia of Integer Sequences."
Zsigmondy, K. "Zur Theorie der Potenzreste." Monatshefte für Math. u. Phys. 3, 265-284, 1882.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|