


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-9-2020
Date: 16-8-2020
Date: 16-7-2020
|
A prime 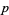 is said to be a Sophie Germain prime if both
is said to be a Sophie Germain prime if both 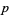 and
and 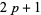 are prime. The first few Sophie Germain primes are 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, ... (OEIS A005384). It is not known if there are an infinite number of Sophie Germain primes (Hoffman 1998, p. 190).
are prime. The first few Sophie Germain primes are 2, 3, 5, 11, 23, 29, 41, 53, 83, 89, 113, 131, ... (OEIS A005384). It is not known if there are an infinite number of Sophie Germain primes (Hoffman 1998, p. 190).
The numbers of Sophie Germain primes less than 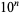 for
for 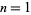 , 2, ... are 3, 10, 37, 190, 1171, 7746, 56032, ... (OEIS A092816).
, 2, ... are 3, 10, 37, 190, 1171, 7746, 56032, ... (OEIS A092816).
The largest known proven Sophie Germain prime pair as of Feb. 29, 2016 is given by 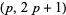 where
where
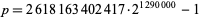 |
(Caldwell), each of which has 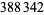 decimal digits (PrimeGrid).
decimal digits (PrimeGrid).
The definition of Sophie Germain primes and the value of the largest then-known such prime were mentioned by the characters Hal and Catherine in the 2005 film Proof.
Sophie Germain primes 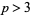 of the form
of the form  correspond to the indices of composite Mersenne numbers
correspond to the indices of composite Mersenne numbers 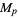 .
.
Around 1825, Sophie Germain proved that the first case of Fermat's last theorem is true for such primes, i.e., if 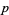 is a Sophie Germain prime, then there do not exist integers
is a Sophie Germain prime, then there do not exist integers  ,
, 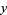 , and
, and 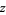 different from 0 and none a multiple of
different from 0 and none a multiple of 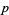 such that
such that
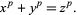 |
REFERENCES:
Caldwell, C. K. "Prime Pages. The Top Twenty: Sophie Germain." https://primes.utm.edu/top20/page.php?id=2#records.
Caldwell, C. K. "The Largest Known Primes!." https://primes.utm.edu/primes/page.php?id=121330 and https://primes.utm.edu/primes/page.php?id=121331.
Dubner, H. "Large Sophie Germain Primes." Math. Comput. 65, 393-396, 1996.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, p. 190, 1998.
Indlekofer, K. H. and Járai, A. "Largest Known Twin Primes and Sophie Germain Primes." Math. Comput. 68, 1317-1324, 1999.
Minovic, P. "RE: Record Sophie Germain Prime Pair." Jan 11, 2005. https://groups.yahoo.com/group/primenumbers/message/15873.
PrimeGrid. "PrimeGrid Primes: Subproject: (SGS) Sophie Germain Prime Search." https://www.primegrid.com/primes/primes.php?project=SGS.
Ribenboim, P. "Sophie Germain Primes." §5.2 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 329-332, 1996.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 154-157, 1993.
Sloane, N. J. A. Sequences A005384/M0731 and A092816 in "The On-Line Encyclopedia of Integer Sequences."
Underbakke, D. "Record Sophie Germain Prime Pair." Jan 11, 2005. https://groups.yahoo.com/group/primenumbers/message/15872.
Underwood, P. "Sophie Germain Record Primes." Message to primeform e-mail list. May 3, 2006. https://groups.yahoo.com/group/primeform/message/7378.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
دراسة تستعرض آلام السجناء السياسيين في حقبة البعث المجرم في العراق
|
|
|