Jacobi Symbol
المؤلف:
Bach, E. and Shallit, J
المصدر:
Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press
الجزء والصفحة:
...
23-8-2020
1875
Jacobi Symbol
The Jacobi symbol, written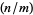 
or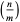 
is defined for positive odd 
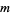as
 |
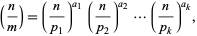(1)
|
where
 |
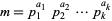(2)
|
is the prime factorization of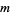 
and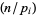 
is the Legendre symbol. (The Legendre symbol is equal to 
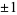depending on whether 
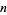is a quadratic residue modulo 
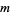.) Therefore, when 
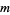is a prime, the Jacobi symbol reduces to the Legendre symbol. Analogously to the Legendre symbol, the Jacobi symbol is commonly generalized to have value
 |
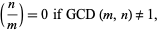(3)
|
giving
 |
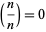(4)
|
as a special case. Note that the Jacobi symbol is not defined f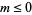or 
or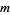 
even. The Jacobi symbol is implemented in the Wolfram Language as JacobiSymbol[n, m].
Use of the Jacobi symbol provides the generalization of the quadratic reciprocity theorem
 |
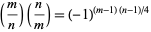(5)
|
for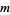 
and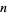 
relatively prime odd integers with 
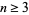(Nagell 1951, pp. 147-148). Written another way,
 |
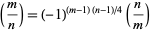(6)
|
or
![(n/m)=<span style=]() {(m/n) for m or n=1 (mod 4); -(m/n) for m,n=3 (mod 4). " src="https://mathworld.wolfram.com/images/equations/JacobiSymbol/NumberedEquation7.gif" style="height:74px; width:227px" /> |
(7)
|
The Jacobi symbol satisfies the same rules as the Legendre symbol
 |
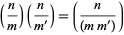(8)
|
 |
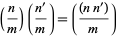(9)
|
 |
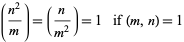(10)
|
 |
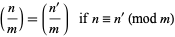(11)
|
![((-1)/m)=(-1)^((m-1)/2)=<span style=]() {1 for m=1 (mod 4); -1 for m=-1 (mod 4) " src="https://mathworld.wolfram.com/images/equations/JacobiSymbol/NumberedEquation12.gif" style="height:41px; width:278px" /> |
(12)
|
![(2/m)=(-1)^((m^2-1)/8)=<span style=]() {1 for m=+/-1 (mod 8); -1 for m=+/-3 (mod 8) " src="https://mathworld.wolfram.com/images/equations/JacobiSymbol/NumberedEquation13.gif" style="height:41px; width:279px" /> |
(13)
|
Bach and Shallit (1996) show how to compute the Jacobi symbol in terms of the simple continued fraction of a rational number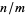 
.
REFERENCES:
Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, pp. 343-344, 1996.
Bressoud, D. M. and Wagon, S. A Course in Computational Number Theory. London: Springer-Verlag, p. 189, 2000.
Guy, R. K. "Quadratic Residues. Schur's Conjecture." §F5 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 244-245, 1994.
Nagell, T. "Jacobi's Symbol and the Generalization of the Reciprocity Law." §42 in Introduction to Number Theory. New York: Wiley, pp. 145-149, 1951.
Riesel, H. "Jacobi's Symbol." Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 281-284, 1994.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
