Tau Function

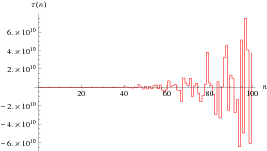
A function 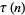 related to the divisor function 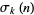, also sometimes called Ramanujan's tau function. It is defined via the Fourier series of the modular discriminant  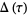for 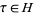, where  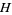is the upper half-plane, by

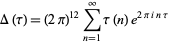(1)

(Apostol 1997, p. 20). The tau function is also given by the Cauchy product

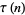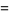			(2)
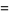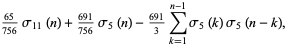			(3)

where 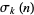 is the divisor function (Apostol 1997, pp. 24 and 140), 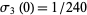, and .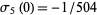

The tau function has generating function

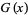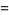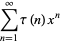			(4)
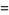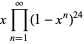			(5)
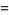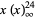			(6)
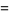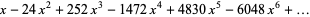			(7)
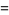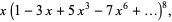			(8)

where 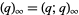 is a q-Pochhammer symbol. The first few values are 1, 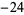, 252, 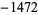, 4830, ... (OEIS A000594). The tau function is given by the Wolfram Language function RamanujanTau[n].

The series

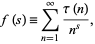(9)

is known as the tau Dirichlet series.

Lehmer (1947) conjectured that 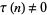 for all 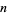, an assertion sometimes known as Lehmer's conjecture. Lehmer verified the conjecture for  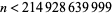(Apostol 1997, p. 22). The following table summarizes progress on finding successively larger values of  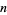for which this condition holds.

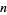	reference
3316799	Lehmer (1947)
214928639999	Lehmer (1949)
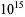	Serre (1973, p. 98), Serre (1985)
1213229187071998	Jennings (1993)
22689242781695999	Jordan and Kelly (1999)
22798241520242687999	Bosman (2007)

Ramanujan gave the computationally efficient triangular recurrence formula

(10)

where

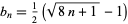(11)

(Lehmer 1943; Jordan and Kelly 1999), which can be used recursively with the formula

(12)

(Gandhi 1961, Jordan and Kelly 1999).

Ewell (1999) gave the beautiful formulas

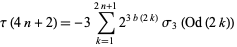	(13)
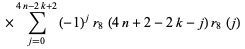	(14)
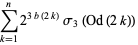	(15)
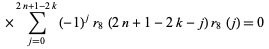	(16)
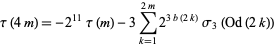	(17)
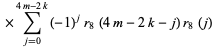	(18)
	(19)
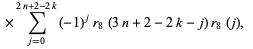	(20)

where 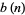 is the exponent of the exact power of 2 dividing 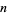,  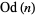is the odd part of 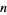,  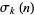is the divisor function of 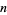, and 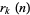 is the sum of squares function.

For prime ,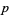

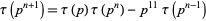(21)

for 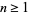, and

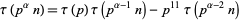(22)

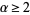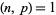for  and  (Mordell 1917; Apostol 1997, p. 92).

Ramanujan conjectured and Mordell (1917) proved that if 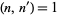, then

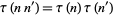(23)

(Hardy 1999, p. 161). More generally,

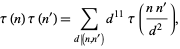(24)

which reduces to the first form if 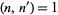 (Mordell 1917; Apostol 1997, p. 93).

Ramanujan (1920) showed that

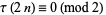	(25)
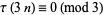	(26)
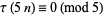	(27)

(Darling 1921; Wilton 1930),

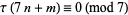(28)

for 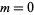 or one the quadratic non-residues of 7, i.e., 3, 5, 6, and

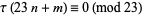(29)

for one the quadratic non-residues of 23, i.e., 5, 7, 10, 11, 14, 15, 17, 19, 20, 21, 22 (Mordell 1922; Wilton 1930). Ewell (1999) showed that

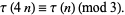(30)

Ramanujan conjectured and Watson proved that 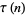 is divisible by 691 for almost all 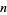, specifically

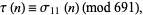(31)

where 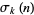 is the divisor function (Wilton 1930; Apostol 1997, pp. 93 and 140; Jordan and Kelly 1999), and 691 is the numerator of the Bernoulli number .

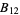Additional congruences include

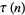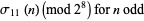			(32)
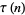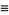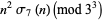			(33)
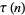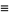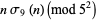			(34)
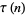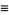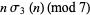			(35)
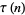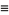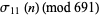			(36)
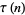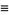			(37)
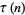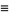			(38)
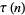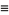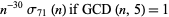			(39)
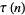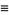			(40)
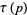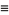			(41)

where 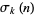 is the divisor function (Swinnerton-Dyer 1988, Jordan and Kelly 1999).

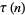 is almost always divisible by  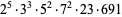according to Ramanujan. In fact, Serre has shown that  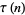is almost always divisible by any integer (Andrews et al. 1988).

The summatory tau function is given by

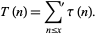(42)

Here, the prime indicates that when  is an integer, the last term 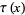 should be replaced by .

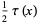REFERENCES:

Andrews, G. E.; Berndt, B. C.; and Rankin, R. A. (Eds.). Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 New York: Academic Press, 1988.

Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, 1997.

Charles, C. D. "Computing the Ramanujan Tau Function." https://www.cs.wisc.edu/~cdx/.

Darling, H. B. C. Proc. London Math. Soc. 19, 350-372, 1921.

Ewell, J. A. "New Representations of Ramanujan's Tau Function." Proc. Amer. Math. Soc. 128, 723-726, 1999.

Gandhi, J. M. "The Nonvanishing of Ramanujan's -Function." Amer. Math. Monthly 68, 757-760, 1961.

Hardy, G. H. "Ramanujan's Function 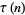." Ch. 10 in Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 63 and 161-185, 1999.

Jennings, D. Ph.D. thesis. Southampton, 1993.

Jordan, B. and Kelly, B. III. "The Vanishing of the Ramanujan Tau Function." Preprint, 12 Mar 1999.

Keiper, J. "On the Zeros of the Ramanujan -Dirichlet Series in the Critical Strip." Math. Comput. 65, 1613-1619, 1996.

LeVeque, W. J. §F35 in Reviews in Number Theory 1940-1972. Providence, RI: Amer. Math. Soc., 1974.

Lehmer, D. H. "Ramanujan's Function 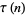." Duke Math. J. 10, 483-492, 1943.

Lehmer, D. H. "The Vanishing of Ramanujan's Function 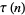." Duke Math. J. 14, 429-433, 1947.

Moreno, C. J. "A Necessary and Sufficient Condition for the Riemann Hypothesis for Ramanujan's Zeta Function." Illinois J. Math. 18, 107-114, 1974.

Mordell, L. J. "On Mr. Ramanujan's Empirical Expansions of Modular Functions." Proc. Cambridge Phil. Soc. 19, 117-124, 1917.

Mordell, L. J. "Note on Certain Modular Relations Considered by Messrs Ramanujan, Darling, and Rogers." Proc. London Math. Soc. 20, 408-416, 1922.

Ramanujan, S. Proc. London Math. Soc. 18, 1920.

Ramanujan, S. "Congruence Properties of Partitions." Math. Z. 9, 147-153, 1921.

Serre, J.-P. A Course in Arithmetic. New York: Springer-Verlag, 1973.

Serre, J.-P. "Sur la Lacunatité des Puissances de 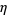." Glasgow Math. J. 27, 203-221, 1985.

Sivaramakrishnan, R. Classical Theory of Arithmetic Functions. New York: Dekker, pp. 275-278, 1989.

Sloane, N. J. A. Sequence A000594/M5153 in "The On-Line Encyclopedia of Integer Sequences."

Spira, R. "Calculation of the Ramanujan Tau-Dirichlet Series." Math. Comput. 27, 379-385, 1973.

Stanley, G. K. "Two Assertions Made by Ramanujan." J. London Math. Soc. 3, 232-237, 1928.

Stanley, G. K. Corrigendum to "Two Assertions Made by Ramanujan." J. London Math. Soc. 4, 32, 1929.

Swinnerton-Dyer, H. P. F. "Congruence Properties of 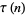." In Ramanujan Revisited: Proceedings of the Centenary Conference, University of Illinois at Urbana-Champaign, June 1-5, 1987 (Ed. G. E. Andrews, B. C. Berndt, and R. A. Rankin). New York: Academic Press, 1988.

Watson, G. N. "Über Ramanujansche Kongruenzeigenschaften der Zerfällungsanzahlen." Math. Z. 39, 712-731, 1935.

Wilton, J. R. "Congruence Properties of Ramanujan's Function 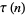." Proc. London Math. Soc. 31, 1-17, 1930.

Yoshida, H. "On Calculations of Zeros of L-Functions Related with Ramanujan's Discriminant Function on the Critical Line." J. Ramanujan Math. Soc. 3, 87-95, 1988.