
Fractional Part
 المؤلف:
Finch, S. R
المؤلف:
Finch, S. R
 المصدر:
"Powers of 3/2 Modulo One." §2.30.1 in Mathematical Constants. Cambridge, England: Cambridge University Press
المصدر:
"Powers of 3/2 Modulo One." §2.30.1 in Mathematical Constants. Cambridge, England: Cambridge University Press
 الجزء والصفحة:
...
الجزء والصفحة:
...
 20-8-2020
20-8-2020
 1442
1442
Fractional Part
The function 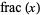 giving the fractional (noninteger) part of a real number
giving the fractional (noninteger) part of a real number  . The symbol
. The symbol ![<span style=]() {x}" src="https://mathworld.wolfram.com/images/equations/FractionalPart/Inline3.gif" style="height:15px; width:17px" /> is sometimes used instead of
{x}" src="https://mathworld.wolfram.com/images/equations/FractionalPart/Inline3.gif" style="height:15px; width:17px" /> is sometimes used instead of 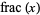 (Graham et al. 1994, p. 70; Havil 2003, p. 109), but this notation is not used in this work due to possible confusion with the set containing the element
(Graham et al. 1994, p. 70; Havil 2003, p. 109), but this notation is not used in this work due to possible confusion with the set containing the element  .
.
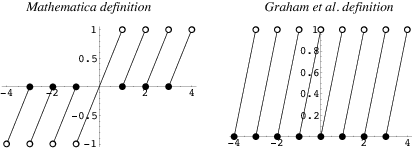
Unfortunately, there is no universal agreement on the meaning of 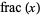 for
for 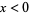 and there are two common definitions. Let
and there are two common definitions. Let 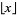 be the floor function, then the Wolfram Language command FractionalPart[x] is defined as
be the floor function, then the Wolfram Language command FractionalPart[x] is defined as
![frac(x)=<span style=]() {x-|_x_| x>=0; x-[x] x<0 " src="https://mathworld.wolfram.com/images/equations/FractionalPart/NumberedEquation1.gif" style="height:41px; width:150px" /> {x-|_x_| x>=0; x-[x] x<0 " src="https://mathworld.wolfram.com/images/equations/FractionalPart/NumberedEquation1.gif" style="height:41px; width:150px" /> |
(1)
|
(left figure). This definition has the benefit that 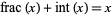 , where
, where 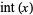 is the integer part of
is the integer part of  . Although Spanier and Oldham (1987) use the same definition as the Wolfram Language, they mention the formula only very briefly and then say it will not be used further. Graham et al. (1994, p. 70), and perhaps most other mathematicians, use the different definition
. Although Spanier and Oldham (1987) use the same definition as the Wolfram Language, they mention the formula only very briefly and then say it will not be used further. Graham et al. (1994, p. 70), and perhaps most other mathematicians, use the different definition
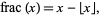 |
(2)
|
(right figure).
The fractional part function can also be extended to the complex plane as
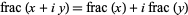 |
(3)
|
as illustrated above.
Since usage concerning fractional part/value and integer part/value can be confusing, the following table gives a summary of names and notations used. Here, S&O indicates Spanier and Oldham (1987).
| notation |
name |
S&O |
Graham et al. |
Wolfram Language |
![[x]](https://mathworld.wolfram.com/images/equations/FractionalPart/Inline12.gif) |
ceiling function |
-- |
ceiling, least integer |
Ceiling[x] |
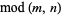 |
congruence |
-- |
-- |
Mod[m, n] |
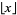 |
floor function |
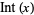 |
floor, greatest integer, integer part |
Floor[x] |
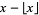 |
fractional value |
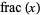 |
fractional part or ![<span style=]() {x}" src="https://mathworld.wolfram.com/images/equations/FractionalPart/Inline18.gif" style="height:15px; width:17px" /> {x}" src="https://mathworld.wolfram.com/images/equations/FractionalPart/Inline18.gif" style="height:15px; width:17px" /> |
SawtoothWave[x] |
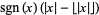 |
fractional part |
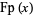 |
no name |
FractionalPart[x] |
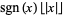 |
integer part |
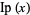 |
no name |
IntegerPart[x] |
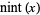 |
nearest integer function |
-- |
-- |
Round[x] |
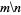 |
quotient |
-- |
-- |
Quotient[m, n] |
The (possibly scaled) periodic waveform corresponding to the latter definition is known as the sawtooth wave.
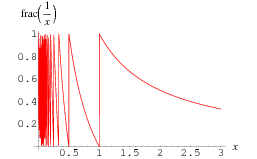
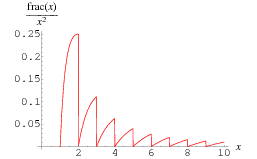
The fractional part of 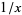 , illustrated above, has the interesting analytic integrals
, illustrated above, has the interesting analytic integrals
The integral
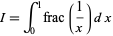 |
(10)
|
is therefore a telescoping sum given by
where 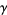 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 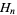 is the harmonic number.
is the harmonic number.
An additional related integral that can be done in closed form and gives the same result is
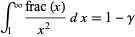 |
(14)
|
(Havil 2003, pp. 109-111).
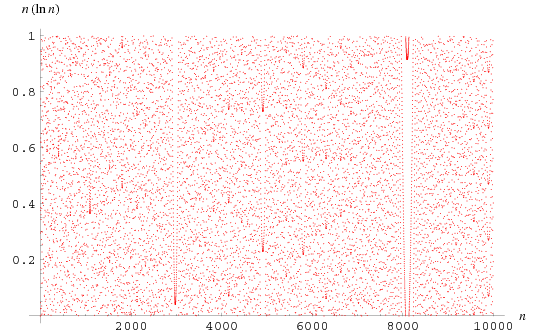
The plot above shows the fractional parts of 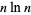 for
for 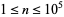 , showing characteristic gaps (Trott 2004, p. 223).
, showing characteristic gaps (Trott 2004, p. 223).
A consequence of Weyl's criterion is that the sequence ![<span style=]() {frac(nx)}" src="https://mathworld.wolfram.com/images/equations/FractionalPart/Inline57.gif" style="height:15px; width:60px" /> is dense and equidistributed in the interval
{frac(nx)}" src="https://mathworld.wolfram.com/images/equations/FractionalPart/Inline57.gif" style="height:15px; width:60px" /> is dense and equidistributed in the interval ![[0,1]](https://mathworld.wolfram.com/images/equations/FractionalPart/Inline58.gif) for irrational
for irrational  , where
, where 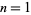 , 2, ... (Finch 2003).
, 2, ... (Finch 2003).
REFERENCES:
Finch, S. R. "Powers of 3/2 Modulo One." §2.30.1 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 194-199, 2003.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 109-110, 2003.
Miklavc, A. "Elementary Proofs of Two Theorems on the Distribution of Numbers ![<span style=]() {nx}" src="https://mathworld.wolfram.com/images/equations/FractionalPart/Inline61.gif" style="height:15px; width:27px" /> (mod 1)." Proc. Amer. Math. Soc. 39, 279-280, 1973.
{nx}" src="https://mathworld.wolfram.com/images/equations/FractionalPart/Inline61.gif" style="height:15px; width:27px" /> (mod 1)." Proc. Amer. Math. Soc. 39, 279-280, 1973.
Sloane, N. J. A. Sequence A000079/M1129 in "The On-Line Encyclopedia of Integer Sequences."
Spanier, J. and Oldham, K. B. "The Integer-Value Int( ) and Fractional-Value frac(
) and Fractional-Value frac( ) Functions." Ch. 9 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 71-78, 1987.
) Functions." Ch. 9 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 71-78, 1987.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. https://www.mathematicaguidebooks.org/.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


