The third prime number, which is also the second Fermat prime, the third Sophie Germain prime, and Fibonacci number 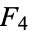. It is an Eisenstein prime, but not a Gaussian prime, since it factors as 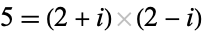. It is the hypotenuse of the smallest Pythagorean triple: 3, 4, 5. For the Pythagorean school, the number 5 was the number of marriage, since it is was the sum of the first female number (2) and the first male number (3). The magic symbol of the pentagram was also based on number 5; it is a star polygon with the smallest possible number of sides, and is formed by the diagonals of a regular pentagon. These intersect each other according to the golden ratio .

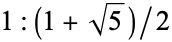There are five Platonic solids. In algebra, five arises in Abel's impossibility theorem as the smallest degree for which an algebraic equation with general coefficients is not solvable by radicals. According to Galois theory, this property is a consequence of the fact that 5 is the smallest positive integer 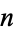 such that the symmetric group  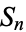is not a solvable group. Five is also the largest positive integer  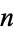such that every finite group of order  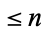is Abelian.

According to Weyl (1952; Chandrasekharan 1986) the five-fold symmetry is typical of plants and animals, whereas it does not appear in the inanimate world.

Words referring to number five often start with the prefix penta- (in Greek 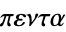-), whereas terms like quintic and quintuple are derived from the Latin quintus (fifth).

REFERENCES:

Chandrasekharan, K. Hermann Weyl (1885-1985): Centenary Lectures. Berlin: Springer-Verlag, 1986.

Weyl, H. Symmetry. Princeton, NJ: Princeton University Press, 1952.

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 58-67, 1986.

اخر الاخبار

اخبار العتبة العباسية المقدسة

بمشاركة الأمين العام للعتبة العبّاسية المقدّسة.. موكب عزاء السادة الخَدَم يحيي ليلة عاشوراء

صحفيّون يشيدون بالتسهيلات الإعلامية التي تقدّمها العتبة العباسية المقدّسة خلال زيارة عاشوراء

أهالي كربلاء ينظّمون مسيرة الشموع الحسينية إحياءً لليلة العاشر من شهر المحرّم

عبر مجلس عزاء.. العتبة العباسية المقدّسة تحيي ليلة اليوم العاشر من المحرّم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد