PSLQ Algorithm

An algorithm which can be used to find integer relations between real numbers 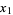, ...,  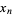such that

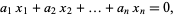with not all 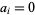. Although the algorithm operates by manipulating a lattice, it does not reduce it to a short vector basis, and is therefore not a lattice reduction algorithm. PSLQ is based on a partial sum of squares scheme (like the PSOS algorithm) implemented using QR decomposition. It was developed by Ferguson and Bailey (1992). A much simplified version of the algorithm was subsequently developed by Ferguson et al. (1999), which also extends the algorithm to complex numbers and quaternions. Ferguson et al. (1999) also demonstrated that PSLQ is distinct from the HJLS algorithm.

The PSLQ algorithm terminates after a number of iterations bounded by a polynomial in 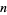 and uses a numerically stable matrix reduction procedure (Ferguson and Bailey 1992). PSLQ tends to be faster than the Ferguson-Forcade algorithm and LLL algorithm because of clever techniques that allow machine arithmetic to be used at many intermediate steps. The LLL algorithm, by comparison, must use moderate precision, although generally not as much as the HJLS algorithm.

While the LLL algorithm is a more general lattice reduction algorithm than PSLQ, using LLL to obtain integer relations is in some sense a "trick," whereas with PSLQ one gets either a relation or lower bounds on degrees of polynomials and sizes of coefficients for which such a relation must satisfy.

REFERENCES:

Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. "Integer Relation Detection." §2.2 in Experimental Mathematics in Action. Wellesley, MA: A K Peters, pp. 29-31, 2007.

Bailey, D. H.; Borwein, J. M.; and Girgensohn, R. "Experimental Evaluation of Euler Sums." Exper. Math. 3, 17-30, 1994.

Bailey, D. H. and Broadhurst, D. J. "Parallel Integer Relation Detection: Techniques and Applications." Math. Comput. 70, 1719-1736, 2000.

Bailey, D. H. "Integer Relation Detection." Computing in Science and Engineering 2, 24-28, 2000.

Bailey, D. and Plouffe, S. "Recognizing Numerical Constants." Organic Mathematics. Proceedings of the Workshop Held in Burnaby, BC, December 12-14, 1995 (Ed. J. Borwein, P. Borwein, L. Jörgenson, and R. Corless). Providence, RI: Amer. Math. Soc., pp. 73-88, 1997. https://www.cecm.sfu.ca/organics/papers/bailey/.

Bertok, P. "PSLQ Integer Relation Algorithm Implementation." https://library.wolfram.com/infocenter/MathSource/4263/.

Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 51-54, 2003.

Borwein, J. M. and Corless, R. M. "Emerging Tools for Experimental Mathematics." Amer. Math. Monthly 106, 899-909, 1999.

Centre for Experimental & Constructive Mathematics. "Integer Relations." https://www.cecm.sfu.ca/projects/IntegerRelations/.

Crandall, R. E. Topics in Advanced Scientific Computation. New York: Springer-Verlag, 1996.

Ferguson, H. R. P. and Bailey, D. H. "A Polynomial Time, Numerically Stable Integer Relation Algorithm." RNR Techn. Rept. RNR-91-032, Jul. 14, 1992.

Ferguson, H. R. P.; Bailey, D. H.; and Arno, S. "Analysis of PSLQ, An Integer Relation Finding Algorithm." Math. Comput. 68, 351-369, 1999.

Zimmerman, P. "Implementation of PSLQ in GMP." https://www.loria.fr/~zimmerma/free/pslq-1.0.c.