Greatest Common Divisor
The greatest common divisor, sometimes also called the highest common divisor (Hardy and Wright 1979, p. 20), of two positive integers  and
and  is the largest divisor common to
is the largest divisor common to  and
and  . For example,
. For example, 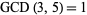 ,
, 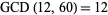 , and
, and 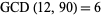 . The greatest common divisor
. The greatest common divisor 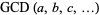 can also be defined for three or more positive integers as the largest divisor shared by all of them. Two or more positive integers that have greatest common divisor 1 are said to be relatively prime to one another, often simply just referred to as being "relatively prime."
can also be defined for three or more positive integers as the largest divisor shared by all of them. Two or more positive integers that have greatest common divisor 1 are said to be relatively prime to one another, often simply just referred to as being "relatively prime."
Various notational conventions are summarized in the following table.
| notation |
source |
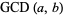 |
this work, Zwillinger (1996, p. 91), Råde and Westergren (2004, p. 54) |
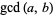 |
Gellert et al. (1989, p. 25), D'Angelo and West (1990, p. 13), Graham et al. (1990, p. 103), Bressoud and Wagon (2000, p. 7), Yan (2002, p. 30), Bronshtein et al. (2007, pp. 323-324), Wolfram Language |
g.c.d.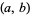 |
Andrews 1994, p. 22 |
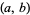 |
|
The greatest common divisor of 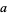 ,
, 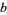 , ... is implemented in the Wolfram Language as GCD[a, b, ...].
, ... is implemented in the Wolfram Language as GCD[a, b, ...].
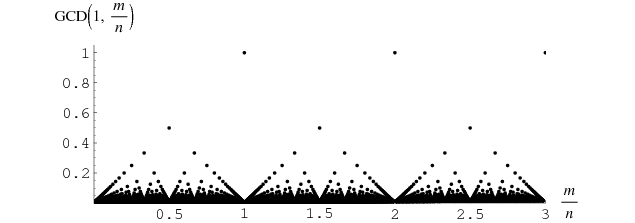
The plot above shows 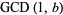 with rational
with rational 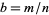 . Here,
. Here, 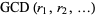 is the greatest rational number
is the greatest rational number 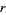 for which all the
for which all the 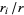 are integers. It is easy to see that if
are integers. It is easy to see that if 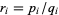 , where
, where 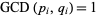 , then
, then 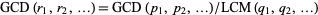 . Furthermore, if
. Furthermore, if 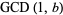 is extended by setting it equal to 0 if
is extended by setting it equal to 0 if 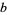 is irrational, the resulting function is continuous at the irrationals, discontinuous at the rationals, and has Riemann integral equal to 0 over any finite interval.
is irrational, the resulting function is continuous at the irrationals, discontinuous at the rationals, and has Riemann integral equal to 0 over any finite interval.

The above plots show a number of visualizations of 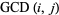 in the
in the 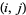 -plane. The figure on the left is simply
-plane. The figure on the left is simply 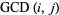 , the figure in the middle is the absolute values of the two-dimensional discrete Fourier transform of
, the figure in the middle is the absolute values of the two-dimensional discrete Fourier transform of 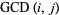 (Trott 2004, pp. 25-26), and the figure at right is the absolute value of the transform of
(Trott 2004, pp. 25-26), and the figure at right is the absolute value of the transform of 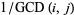 .
.
If 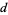 is the greatest common divisor of
is the greatest common divisor of 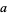 and
and 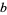 , then
, then 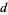 is the largest possible integer satisfying
is the largest possible integer satisfying
with  and
and 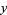 positive integers.
positive integers.
The Euclidean algorithm can be used to find the greatest common divisor of two integers and to find integers  and
and 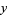 such that
such that
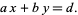 |
(3)
|
The notion can also be generalized to more general rings than simply the integers 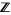 . However, even for Euclidean rings, the notion of GCD of two elements of a ring is not the same as the GCD of two ideals of a ring. This is sometimes a source of confusion when studying rings other than
. However, even for Euclidean rings, the notion of GCD of two elements of a ring is not the same as the GCD of two ideals of a ring. This is sometimes a source of confusion when studying rings other than 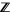 , such as polynomial rings in several variables.
, such as polynomial rings in several variables.
To compute the GCD, write the prime factorizations of 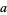 and
and 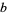 ,
,
where the 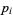 s are all prime factors of
s are all prime factors of 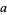 and
and 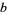 , and if
, and if 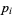 does not occur in one factorization, then the corresponding exponent is taken as 0. Then the greatest common divisor
does not occur in one factorization, then the corresponding exponent is taken as 0. Then the greatest common divisor 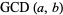 is given by
is given by
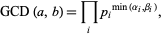 |
(6)
|
where min denotes the minimum. For example, consider 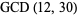 .
.
so
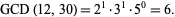 |
(9)
|
The GCD is distributive
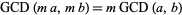 |
(10)
|
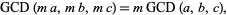 |
(11)
|
and associative
If 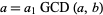 and
and 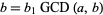 , then
, then
so 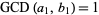 . The GCD is also idempotent
. The GCD is also idempotent
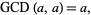 |
(17)
|
commutative
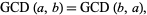 |
(18)
|
and satisfies the absorption law
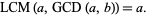 |
(19)
|

A recurrence equation that converges to 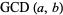 for positive odd
for positive odd 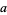 and
and 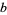 is given by
is given by
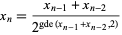 |
(20)
|
with 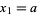 and
and 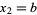 , where
, where 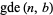 is the greatest dividing exponent of
is the greatest dividing exponent of 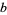 in
in 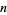 (Stehlé and Zimmerman 2004). The plot above shows the number of iterations required to converge for odd
(Stehlé and Zimmerman 2004). The plot above shows the number of iterations required to converge for odd 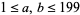 .
.
The probability that two integers picked at random are relatively prime is ![[zeta(2)]^(-1)=6/pi^2](https://mathworld.wolfram.com/images/equations/GreatestCommonDivisor/Inline93.gif) , where
, where 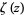 is the Riemann zeta function. Polezzi (1997) observed that
is the Riemann zeta function. Polezzi (1997) observed that 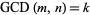 , where
, where 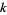 is the number of lattice points in the plane on the straight line connecting the vectors (0, 0) and
is the number of lattice points in the plane on the straight line connecting the vectors (0, 0) and 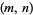 (excluding
(excluding 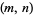 itself). This observation is intimately connected with the probability of obtaining relatively prime integers, and also with the geometric interpretation of a reduced fraction
itself). This observation is intimately connected with the probability of obtaining relatively prime integers, and also with the geometric interpretation of a reduced fraction 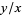 as a string through a lattice of points with ends at (1,0) and
as a string through a lattice of points with ends at (1,0) and 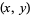 . The pegs it presses against
. The pegs it presses against 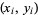 give alternate convergents
give alternate convergents 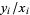 of the continued fraction for
of the continued fraction for 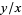 , while the other convergents are obtained from the pegs it presses against with the initial end at (0, 1).
, while the other convergents are obtained from the pegs it presses against with the initial end at (0, 1).
Knuth showed that
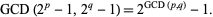 |
(21)
|
REFERENCES:
Andrews, G. E. Number Theory. New York: Dover, 1994.
Bressoud, D. M. and Wagon, S. A Course in Computational Number Theory. London: Springer-Verlag, 2000.
Bronshtein, I. N.; Semendyayev, K. A.; Musiol, G.; and Muehlig, H. Handbook of Mathematics, 5th ed. Berlin: Springer-Verlag, 2007.
D'Angelo, J. P. and West, D. B. Mathematical Thinking: Problem-Solving and Proofs, 2nd ed. Upper Saddle River, NJ: Prentice-Hall, 2000.
Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, 1989.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science. Reading, MA: Addison-Wesley, 1990.
Nagell, T. "Least Common Multiple and Greatest Common Divisor." §5 in Introduction to Number Theory. New York: Wiley, pp. 16-19, 1951.
Polezzi, M. "A Geometrical Method for Finding an Explicit Formula for the Greatest Common Divisor." Amer. Math. Monthly 104, 445-446, 1997.
Råde, L. and Westergren, B. Mathematics Handbook for Science and Engineering. Berlin: Springer-Verlag, 2004.
Séroul, R. "The Greatest Common Divisor." §2.4 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 9-11, 2000.
Stehlé, D. and Zimmerman, P. "A Binary Recursive GCD Algorithm." In Algorithmic Number Theory. Proceedings of the 6th International Symposium (ANTS-VI) held at the University of Vermont, Burlington, VT, June 13-18, 2004 (Ed. D. Buell). Berlin: Springer-Verlag, pp. 411-425, 2004.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, pp. 25-26, 2004. https://www.mathematicaguidebooks.org/.
Yan, S. Y. Number Theory for Computing, 2nd ed. Berlin: Springer, 2002.
Zwillinger, D. (Ed.). "Greatest Common Divisor." §2.3.5 in CRC Standard Mathematical Tables and Formulae, 30th ed. Boca Raton, FL: CRC Press, p. 91, 1996.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


