Euclidean Algorithm
The Euclidean algorithm, also called Euclid's algorithm, is an algorithm for finding the greatest common divisor of two numbers 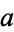 and
and 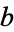 . The algorithm can also be defined for more general rings than just the integers
. The algorithm can also be defined for more general rings than just the integers 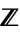 . There are even principal rings which are not Euclidean but where the equivalent of the Euclidean algorithm can be defined. The algorithm for rational numbers was given in Book VII of Euclid's Elements. The algorithm for reals appeared in Book X, making it the earliest example of an integer relation algorithm (Ferguson et al. 1999).
. There are even principal rings which are not Euclidean but where the equivalent of the Euclidean algorithm can be defined. The algorithm for rational numbers was given in Book VII of Euclid's Elements. The algorithm for reals appeared in Book X, making it the earliest example of an integer relation algorithm (Ferguson et al. 1999).
The Euclidean algorithm is an example of a P-problem whose time complexity is bounded by a quadratic function of the length of the input values (Bach and Shallit 1996).
Let 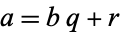 , then find a number
, then find a number 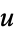 which divides both
which divides both 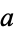 and
and 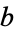 (so that
(so that 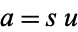 and
and 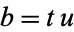 ), then
), then 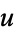 also divides
also divides 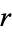 since
since
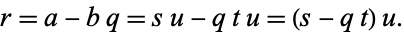 |
(1)
|
Similarly, find a number 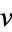 which divides
which divides 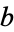 and
and 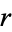 (so that
(so that 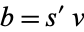 and
and 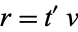 ), then
), then 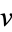 divides
divides 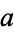 since
since
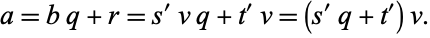 |
(2)
|
Therefore, every common divisor of 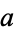 and
and 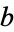 is a common divisor of
is a common divisor of 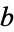 and
and 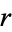 , so the procedure can be iterated as follows:
, so the procedure can be iterated as follows:
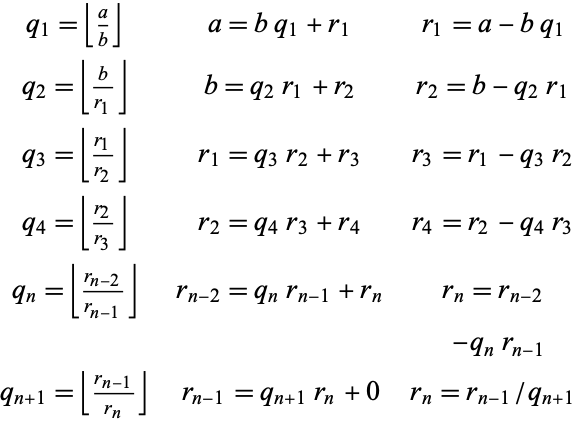 |
(3)
|
For integers, the algorithm terminates when 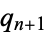 divides
divides 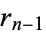 exactly, at which point
exactly, at which point 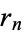 corresponds to the greatest common divisor of
corresponds to the greatest common divisor of 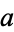 and
and 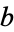 ,
, 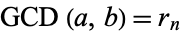 . For real numbers, the algorithm yields either an exact relation or an infinite sequence of approximate relations (Ferguson et al. 1999).
. For real numbers, the algorithm yields either an exact relation or an infinite sequence of approximate relations (Ferguson et al. 1999).
An important consequence of the Euclidean algorithm is finding integers 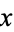 and
and 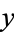 such that
such that
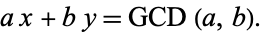 |
(4)
|
This can be done by starting with the equation for 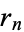 , substituting for
, substituting for 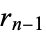 from the previous equation, and working upward through the equations.
from the previous equation, and working upward through the equations.
Note that the 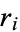 are just remainders, so the algorithm can be easily applied by hand by repeatedly computing remainders of consecutive terms starting with the two numbers of interest (with the larger of the two written first). As an example, consider applying the algorithm to
are just remainders, so the algorithm can be easily applied by hand by repeatedly computing remainders of consecutive terms starting with the two numbers of interest (with the larger of the two written first). As an example, consider applying the algorithm to 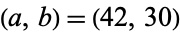 . This gives 42, 30, 12, 6, 0, so
. This gives 42, 30, 12, 6, 0, so 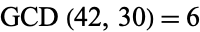 . Similarly, applying the algorithm to (144, 55) gives 144, 55, 34, 21, 13, 8, 5, 3, 2, 1, 0, so
. Similarly, applying the algorithm to (144, 55) gives 144, 55, 34, 21, 13, 8, 5, 3, 2, 1, 0, so 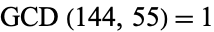 and 144 and 55 are relatively prime.
and 144 and 55 are relatively prime.
A concise Wolfram Language implementation can be given as follows.
Remainder[a_, b_] := Mod[a, b]
Remainder[a_, 0] := 0
EuclideanAlgorithmGCD[a_, b_] := FixedPointList[
{Last[#], Remainder @@ #}&, {a, b}][[-3, 1]]
Lamé showed that the number of steps needed to arrive at the greatest common divisor for two numbers less than 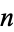 is
is
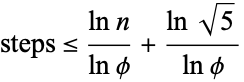 |
(5)
|
where 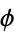 is the golden ratio. Numerically, Lamé's expression evaluates to
is the golden ratio. Numerically, Lamé's expression evaluates to
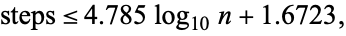 |
(6)
|
which, for 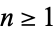 , is always
, is always 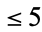 times the number of digits in the smaller number (Wells 1986, p. 59). As shown by Lamé's theorem, the worst case occurs when the algorithm is applied to two consecutive Fibonacci numbers. Heilbronn showed that the average number of steps is
times the number of digits in the smaller number (Wells 1986, p. 59). As shown by Lamé's theorem, the worst case occurs when the algorithm is applied to two consecutive Fibonacci numbers. Heilbronn showed that the average number of steps is 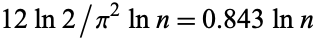 for all pairs
for all pairs 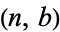 with
with 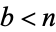 . Kronecker showed that the shortest application of the algorithm uses least absolute remainders. The quotients obtained are distributed as shown in the following table (Wagon 1991).
. Kronecker showed that the shortest application of the algorithm uses least absolute remainders. The quotients obtained are distributed as shown in the following table (Wagon 1991).
| quotient |
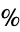 |
| 1 |
41.5 |
| 2 |
17.0 |
| 3 |
9.3 |
Let 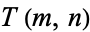 be the number of divisions required to compute
be the number of divisions required to compute 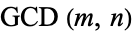 using the Euclidean algorithm, and define
using the Euclidean algorithm, and define 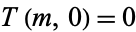 if
if 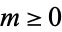 . Then the function
. Then the function 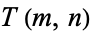 is given by the recurrence relation
is given by the recurrence relation
![T(m,n)=<span style=]() {1+T(n,m mod n) for m>=n; 1+T(n,m) for m<n. " src="https://mathworld.wolfram.com/images/equations/EuclideanAlgorithm/NumberedEquation7.gif" style="height:41px; width:247px" /> {1+T(n,m mod n) for m>=n; 1+T(n,m) for m<n. " src="https://mathworld.wolfram.com/images/equations/EuclideanAlgorithm/NumberedEquation7.gif" style="height:41px; width:247px" /> |
(7)
|
Tabulating this function for 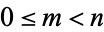 gives
gives
 |
(8)
|
(OEIS A051010). The maximum numbers of steps for a given 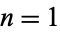 , 2, 3, ... are 1, 2, 2, 3, 2, 3, 4, 3, 3, 4, 4, 5, ... (OEIS A034883).
, 2, 3, ... are 1, 2, 2, 3, 2, 3, 4, 3, 3, 4, 4, 5, ... (OEIS A034883).
Consider the function
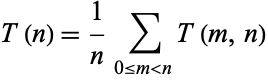 |
(9)
|
giving the average number of steps when 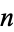 is fixed and
is fixed and 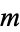 chosen at random (Knuth 1998, pp. 344 and 353-357). The first few values of
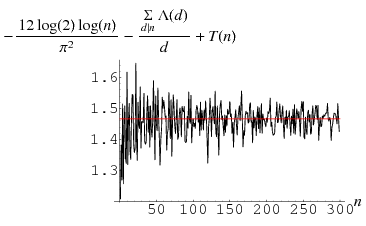
chosen at random (Knuth 1998, pp. 344 and 353-357). The first few values of 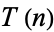 are 0, 1/2, 1, 1, 8/5, 7/6, 13/7, 7/4, ... (OEIS A051011 and A051012). Norton (1990) showed that
are 0, 1/2, 1, 1, 8/5, 7/6, 13/7, 7/4, ... (OEIS A051011 and A051012). Norton (1990) showed that
![T(n)=(12ln2)/(pi^2)[lnn-sum_(d|n)(Lambda(d))/d]+C+1/nsum_(d|n)phi(d)O(d^(-1/6+epsilon)),](https://mathworld.wolfram.com/images/equations/EuclideanAlgorithm/NumberedEquation10.gif) |
(10)
|
where 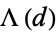 is the Mangoldt function and
is the Mangoldt function and 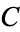 is Porter's constant (Knuth 1998, pp. 355-356).
is Porter's constant (Knuth 1998, pp. 355-356).
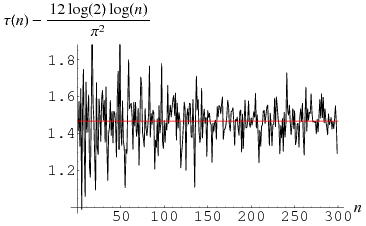
The related function
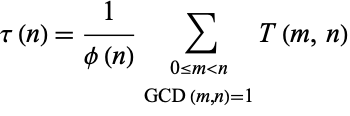 |
(11)
|
where 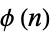 is the totient function, gives the average number of divisions when
is the totient function, gives the average number of divisions when 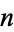 is fixed and
is fixed and 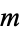 is a random number coprime to
is a random number coprime to 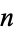 . Porter (1975) showed that
. Porter (1975) showed that
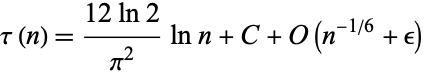 |
(12)
|
(Knuth 1998, pp. 354-355).
Finally, define
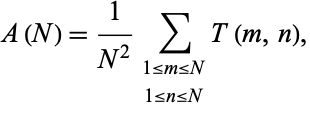 |
(13)
|
as the average number of divisions when 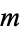 and
and 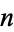 are both chosen at random in
are both chosen at random in ![[1,N]](https://mathworld.wolfram.com/images/equations/EuclideanAlgorithm/Inline63.gif) Norton (1990) proved that
Norton (1990) proved that
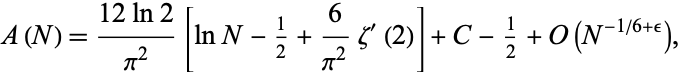 |
(14)
|
where 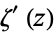 is the derivative of the Riemann zeta function.
is the derivative of the Riemann zeta function.
There exist 21 quadratic fields in which there is a Euclidean algorithm (Inkeri 1947, Barnes and Swinnerton-Dyer 1952).
For additional details, see Uspensky and Heaslet (1939) and Knuth (1998).
Although various attempts were made to generalize the algorithm to find integer relations between 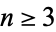 variables, none were successful until the discovery of the Ferguson-Forcade algorithm (Ferguson et al. 1999). Several other integer relation algorithms have now been discovered.
variables, none were successful until the discovery of the Ferguson-Forcade algorithm (Ferguson et al. 1999). Several other integer relation algorithms have now been discovered.
REFERENCES:
Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, 1996.
Barnes, E. S. and Swinnerton-Dyer, H. P. F. "The Inhomogeneous Minima of Binary Quadratic Forms. I." Acta Math 87, 259-323, 1952.
Chabert, J.-L. (Ed.). "Euclid's Algorithm." Ch. 4 in A History of Algorithms: From the Pebble to the Microchip. New York: Springer-Verlag, pp. 113-138, 1999.
Cohen, H. A Course in Computational Algebraic Number Theory. New York: Springer-Verlag, 1993.
Courant, R. and Robbins, H. "The Euclidean Algorithm." §2.4 in Supplement to Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 42-51, 1996.
Dunham, W. Journey through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 69-70, 1990.
Ferguson, H. R. P.; Bailey, D. H.; and Arno, S. "Analysis of PSLQ, An Integer Relation Finding Algorithm." Math. Comput. 68, 351-369, 1999.
Finch, S. R. "Porter-Hansley Constants." §2.18 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 156-160, 2003.
Inkeri, K. "Über den Euklidischen Algorithmus in quadratischen Zahlkörpern." Ann. Acad. Sci. Fennicae. Ser. A. I. Math.-Phys. 1947, 1-35, 1947.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1997.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.
Motzkin, T. "The Euclidean Algorithm." Bull. Amer. Math. Soc. 55, 1142-1146, 1949.
Nagell, T. "Euclid's Algorithm." §7 in Introduction to Number Theory. New York: Wiley, pp. 21-23, 1951.
Norton, G. H. "On the Asymptotic Analysis of the Euclidean Algorithm." J. Symb. Comput. 10, 53-58, 1990.
Porter, J. W. "On a Theorem of Heilbronn." Mathematika 22, 20-28, 1975.
Séroul, R. "Euclidean Division" and "The Euclidean Algorithm." §2.1 and 8.1 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 5 and 169-161, 2000.
Sloane, N. J. A. Sequences A034883, A051010, A051011, and A051012 in "The On-Line Encyclopedia of Integer Sequences."
Uspensky, J. V. and Heaslet, M. A. Elementary Number Theory. New York: McGraw-Hill, 1939.
Wagon, S. "The Ancient and Modern Euclidean Algorithm" and "The Extended Euclidean Algorithm." §8.1 and 8.2 in Mathematica in Action. New York: W. H. Freeman, pp. 247-252 and 252-256, 1991.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 59, 1986.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


