
Steffi Problem
 المؤلف:
Sloane, N. J. A
المؤلف:
Sloane, N. J. A
 المصدر:
Sequences A080202 and A080203 in "The On-Line Encyclopedia of Integer Sequences."
المصدر:
Sequences A080202 and A080203 in "The On-Line Encyclopedia of Integer Sequences."
 الجزء والصفحة:
...
الجزء والصفحة:
...
 30-6-2020
30-6-2020
 1449
1449
Steffi Problem
A homework problem proposed in Steffi's math class in January 2003 asked students to prove that no ratio of two unequal numbers obtained by permuting all the digits 1, 2, ..., 7 results in an integer. If such a ratio 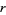 existed, then some permutation of 1234567 would have to be divisible by
existed, then some permutation of 1234567 would have to be divisible by 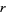 .
. 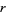 can immediately be restricted to
can immediately be restricted to 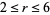 , since a ratio of two permutations of the first seven digits must be less than
, since a ratio of two permutations of the first seven digits must be less than 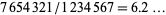 , and the permutations were stated to be unequal, so
, and the permutations were stated to be unequal, so 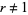 . The case
. The case 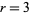 can be eliminated by the divisibility test for 3, which says that a number is divisible by 3 iff the sum of its digits is divisible by 3. Since the sum of the digits 1 to 7 is 28, which is not divisible by 3, there is no permutation of these digits that is divisible by 3. This also eliminates
can be eliminated by the divisibility test for 3, which says that a number is divisible by 3 iff the sum of its digits is divisible by 3. Since the sum of the digits 1 to 7 is 28, which is not divisible by 3, there is no permutation of these digits that is divisible by 3. This also eliminates 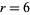 as a possibility, since a number must be divisible by 3 to be divisible by 6.
as a possibility, since a number must be divisible by 3 to be divisible by 6.
This leaves only the cases 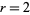 , 4, and 5 to consider. The
, 4, and 5 to consider. The 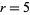 case can be eliminated by noting that in order to be divisible by 5, the last digits of the numerator and denominator must be 5 and 1, respectively
case can be eliminated by noting that in order to be divisible by 5, the last digits of the numerator and denominator must be 5 and 1, respectively
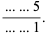 |
(1)
|
The largest possible ratio that can be obtained will then use the largest possible number in the numerator and the smallest possible in the denominator, namely
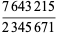 |
(2)
|
But 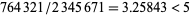 , so it is not possible to construct a fraction that is divisible by 5. Therefore, only
, so it is not possible to construct a fraction that is divisible by 5. Therefore, only 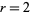 and 4 need now be considered.
and 4 need now be considered.
In general, consider the numbers of pairs of unequal permutations of all the digits 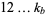 in base
in base 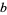 (
(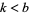 ) whose ratio is an integer. Then there is a unique
) whose ratio is an integer. Then there is a unique 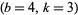 solution
solution
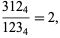 |
(3)
|
a unique 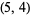 solution
solution
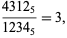 |
(4)
|
three  solutions
solutions
and so on.
The number of solutions for the first few bases and numbers of digits  are summarized in the table below (OEIS A080202).
are summarized in the table below (OEIS A080202).
 |
solutions for digits 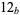 , , 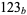 , ..., , ..., 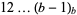 |
| 3 |
0 |
| 4 |
0, 1 |
| 5 |
0, 0, 1 |
| 6 |
0, 0, 3, 25 |
| 7 |
0, 0, 0, 2, 7 |
| 8 |
0, 0, 0, 0, 68, 623 |
| 9 |
0, 0, 0, 0, 0, 124, 1183 |
| 10 |
0, 0, 0, 0, 0, 0, 2338, 24603 |
| 11 |
0, 0, 0, 0, 0, 0, 3, 598, 5895 |
| 12 |
0, 0, 0, 0, 0, 0, 0, 0, 161947, 2017603 |
As can be seen from the table, in base 10, the only solutions are for the digits 12345678 and 123456789. Of the solutions for 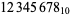 , there are two that produce three different integers for the same numerator:
, there are two that produce three different integers for the same numerator:
Taking the diagonal entries 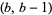 from this list for
from this list for 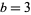 , 4, ... gives the sequence 0, 1, 1, 25, 7, 623, 1183, 24603, ... (OEIS A080203).
, 4, ... gives the sequence 0, 1, 1, 25, 7, 623, 1183, 24603, ... (OEIS A080203).
REFERENCES:
Sloane, N. J. A. Sequences A080202 and A080203 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


