


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-1-2020
Date: 30-10-2019
Date: 24-8-2020
|
Find a square number 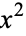 such that, when a given integer
such that, when a given integer 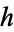 is added or subtracted, new square numbers are obtained so that
is added or subtracted, new square numbers are obtained so that
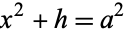 |
(1) |
and
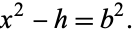 |
(2) |
This problem was posed by the mathematicians Théodore and Jean de Palerma in a mathematical tournament organized by Frederick II in Pisa in 1225. The solution (Ore 1988, pp. 188-191) is
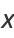 |
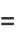 |
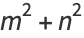 |
(3) |
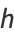 |
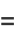 |
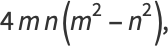 |
(4) |
where 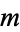 and
and 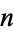 are integers.
are integers. 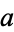 and
and 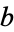 are then given by
are then given by
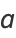 |
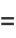 |
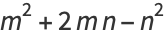 |
(5) |
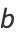 |
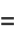 |
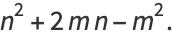 |
(6) |
Fibonacci proved that all numbers 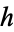 (the congrua) are divisible by 24. Fermat's right triangle theorem is equivalent to the result that a congruum cannot be a square number.
(the congrua) are divisible by 24. Fermat's right triangle theorem is equivalent to the result that a congruum cannot be a square number.
A table for small 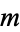 and
and 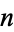 is given in Ore (1988, p. 191), and a larger one (for
is given in Ore (1988, p. 191), and a larger one (for 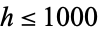 ) by Lagrange (1977). The first
) by Lagrange (1977). The first
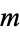 |
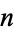 |
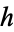 |
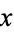 |
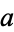 |
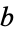 |
| Sloane | A057103 | A055096 | A057104 | A057105 | |
| 2 | 1 | 24 | 5 | 7 | 1 |
| 3 | 1 | 96 | 10 | 14 | 2 |
| 3 | 2 | 120 | 13 | 17 | 7 |
| 4 | 1 | 240 | 17 | 23 | 7 |
| 4 | 2 | 384 | 20 | 28 | 4 |
| 4 | 3 | 336 | 25 | 31 | 17 |
REFERENCES:
Alter, R. and Curtz, T. B. "A Note on Congruent Numbers." Math. Comput. 28, 303-305, 1974.
Alter, R.; Curtz, T. B.; and Kubota, K. K. "Remarks and Results on Congruent Numbers." In Proc. Third Southeastern Conference on Combinatorics, Graph Theory, and Computing, 1972, Boca Raton, FL. Boca Raton, FL: Florida Atlantic University, pp. 27-35, 1972.
Bastien, L. "Nombres congruents." Interméd. des Math. 22, 231-232, 1915.
Gérardin, A. "Nombres congruents." Interméd. des Math. 22, 52-53, 1915.
Lagrange, J. "Construction d'une table de nombres congruents." Calculateurs en Math., Bull. Soc. math. France., Mémoire 49-50, 125-130, 1977.
Ore, Ø. Number Theory and Its History. New York: Dover, 1988.
Sloane, N. J. A. Sequences A055096, A057103, A057104, and A057105 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|