المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Congruent Number |
 939
 05:01 مساءً
date: 18-5-2020 |
Author : Koblitz, N 
Book or Source : Introduction to Elliptic Curves and Modular Forms. New York: Springer-Verlag, 1993. 
Page and Part : ...|
Read More
Date: 19-11-2020
1154
Date: 9-3-2020
860
Date: 19-11-2020
1157
|
A congruent number can be defined as an integer that is equal to the area of a rational right triangle (Koblitz 1993).
Numbers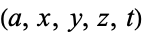 
such that
 |
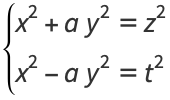(1) |
are also known as congruent numbers. They are a generalization of the congruum problem, which is the case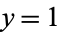 
.
For example,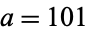 
, the smallest congruent numbers are
 |
 |
 |
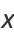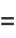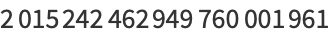(2) |
 |
 |
 |
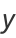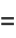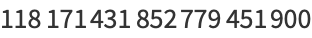(3) |
 |
 |
 |
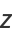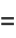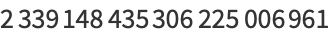(4) |
 |
 |
 |
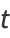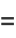(5) |
REFERENCES:
Guy, R. K. "Congruent Number." §D76 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 195-197, 1994.
Koblitz, N. Introduction to Elliptic Curves and Modular Forms. New York: Springer-Verlag, 1993.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
بالصور: تزامنا مع ختام فعالياته.. ممثل المرجعية العليا يشارك في المحفل القرآني المركزي في الصحن الحسيني الشريف
|
|
|
