Archimedes, Recurrence Formula
المؤلف:
Dörrie, H.
المصدر:
100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover
الجزء والصفحة:
...
5-3-2020
1256
Archimedes' Recurrence Formula
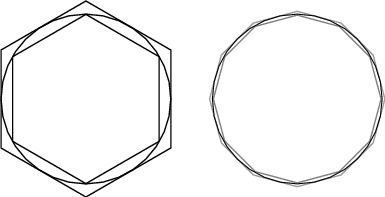
Let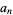 
and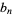 
be the perimeters of the circumscribed and inscribed 
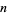-gon 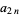and 
and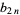 
the perimeters of the circumscribed and inscribed 
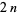-gon. Then
The first follows from the fact that side lengths of the polygons on a circle of radius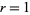 
are
so
But
Using the identity
 |
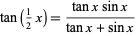(9)
|
then gives
 |
(10)
|
The second follows from
 |
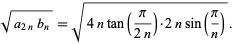(11)
|
Using the identity
 |
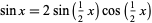(12)
|
gives
Successive application gives the Archimedes algorithm, which can be used to provide successive approximations to pi (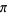
).
REFERENCES:
Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, p. 186, 1965.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
