Sphere tetrahedron picking is the selection of quadruples of of points corresponding to vertices of a tetrahedron with vertices on the surface of a sphere. 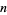 random tetrahedra can be picked on a unit sphere in the Wolfram Language using the function RandomPoint[Sphere[], {" src="http://mathworld.wolfram.com/images/equations/SphereTetrahedronPicking/Inline2.gif" style="height:15px; width:5px" />n, 4}" src="http://mathworld.wolfram.com/images/equations/SphereTetrahedronPicking/Inline3.gif" style="height:15px; width:5px" />].

Pick four points on a sphere. What is the probability that the tetrahedron having these points as polyhedron vertices contains the center of the sphere? In the one-dimensional case, the probability that a second point is on the opposite side of 1/2 is 1/2. In the two-dimensional case, pick two points. In order for the third to form a triangle containing the center, it must lie in the quadrant bisected by a line segment passing through the center of the circle and the bisector of the two points. This happens for one quadrant, so the probability is 1/4. Similarly, for a sphere the probability is one octant, or 1/8.

Pick four points at random on the surface of a unit sphere using

			(1)
			(2)
			(3)

with  and 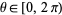. Now find the distribution of possible volumes of the (nonregular) tetrahedra determined by these points. Without loss of generality, the first point may be taken as 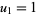, or 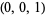, while the second may be taken as 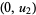, or 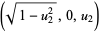. The average volume is then

			(4)
			(5)

where the vertices are located at 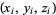 where 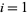, ..., 4, and the (signed) volume is given by the determinant

(6)

The analytic result is difficult to compute, but the exact result for the mean tetrahedron volume is given by

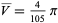(7)

(Miles 1971, Heinrich et al. 1998, Finch 2011). The raw moments can be computed more easily for even 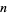, giving

			(8)
			(9)
			(10)
			(11)

REFERENCES:

Buchta, C. "A Note on the Volume of a Random Polytope in a Tetrahedron." Ill. J. Math. 30, 653-659, 1986.

Finch, S. "Random Triangles VI." http://algo.inria.fr/csolve/rtg6.pdf. Jan. 7, 2011.

Heinrich, L.; Körner, R.; Mehlhorn, N.; and Muche, L. "Numerical and Analytical Computation of Some Second-Order Characteristics of Spatial Poisson-Voronoi Tessellations." Statistics 31, 235-259, 1998.

Miles, R. E. "Isotropic Random Simplices." Adv. Appl. Prob. 3, 353-382, 1971.

اخر الاخبار

اخبار العتبة العباسية المقدسة

المجمَع العلمي يطلق الدورة التطويرية الخامسة لمعلمي التربية الإسلامية ومدرسيها في النجف الأشرف

خدمات إنسانية متنوّعة تقدّمها شعبة الشهداء والجرحى في مختلف المحافظات

قسم العلاقات العامة يطلق فعاليات مخيم البذرة الواعدة الخاص بأبناء المنتسبين

جامعة العميد تنظم سلسلة دورات تطويرية لملاكاتها الإدارية

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد