

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Constructible Polygon
المؤلف:
Bachmann, P.
المصدر:
Die Lehre von der Kreistheilung und ihre Beziehungen zur Zahlentheorie. Leipzig, Germany: Teubner, 1872.
الجزء والصفحة:
...
6-2-2020
2971
Constructible Polygon
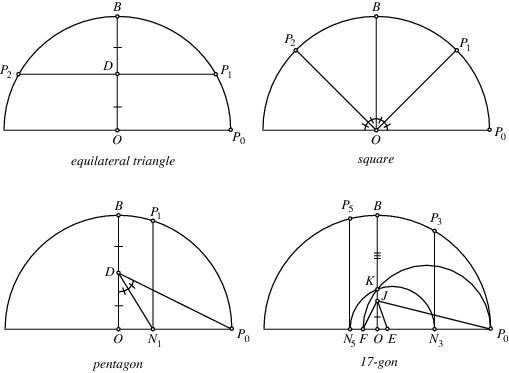
Compass and straightedge geometric constructions dating back to Euclid were capable of inscribing regular polygons of 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 32, 40, 48, 60, 64, ..., sides. In 1796 (when he was 19 years old), Gauss gave a sufficient condition for a regular 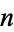 -gon to be constructible, which he also conjectured (but did not prove) to be necessary, thus showing that regular
-gon to be constructible, which he also conjectured (but did not prove) to be necessary, thus showing that regular 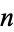 -gons were constructible for
-gons were constructible for 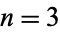 , 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, ... (OEIS A003401).
, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, ... (OEIS A003401).
A complete enumeration of "constructible" polygons is given by those with central angles corresponding to so-called trigonometry angles.
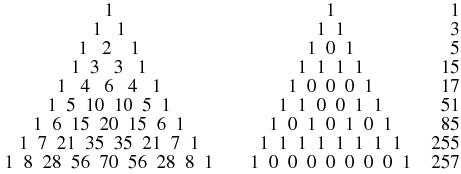
Gardner (1977) and independently Watkins (Conway and Guy 1996, Krížek et al. 2001) noticed that the number of sides for constructible polygons with odd numbers of sides are given by the first 32 rows of the Sierpiński sieve interpreted as binary numbers, giving 1, 3, 5, 15, 17, 51, 85, 255, ... (OEIS A004729, Conway and Guy 1996, p. 140). In other words, every row is a product of distinct Fermat primes, with terms given by binary counting.
REFERENCES:
Bachmann, P. Die Lehre von der Kreistheilung und ihre Beziehungen zur Zahlentheorie. Leipzig, Germany: Teubner, 1872.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 94-96, 1987.
Bold, B. "The Problem of Constructing Regular Polygons." Ch. 7 in Famous Problems of Geometry and How to Solve Them. New York: Dover, pp. 49-71, 1982.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 190-191, 1996.
Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, 1996.
De Temple, D. W. "Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions." Amer. Math. Monthly 98, 97-108, 1991.
Dickson, L. E. "Constructions with Ruler and Compasses; Regular Polygons." Ch. 8 in Monographs on Topics of Modern Mathematics Relevant to the Elementary Field (Ed. J. W. A. Young). New York: Dover, pp. 352-386, 1955.
Dixon, R. "Compass Drawings." Ch. 1 in Mathographics. New York: Dover, pp. 1-78, 1991.
Gardner, M. "Pascal's Triangle." Ch. 15 in Mathematical Carnival: A New Round-Up of Tantalizers and Puzzles from Scientific American. New York: Vintage Books, pp. 194-207, 1977.
Gauss, C. F. §365 and 366 in Disquisitiones Arithmeticae. Leipzig, Germany, 1801. Reprinted New Haven, CT: Yale University Press, 1965.
Heath, T. L. The Thirteen Books of the Elements, 2nd ed., Vol. 2: Books III-IX. New York: Dover, 1956.
Joyce, D. E. "Euclid's Elements." http://aleph0.clarku.edu/~djoyce/java/elements/elements.html.
Kazarinoff, N. D. "On Who First Proved the Impossibility of Constructing Certain Regular Polygons with Ruler and Compass Alone." Amer. Math. Monthly 75, 647-648, 1968.
Klein, F. "The Division of the Circle into Equal Parts." Part I, Ch. 3 in "Famous Problems of Elementary Geometry: The Duplication of the Cube, the Trisection of the Angle, and the Quadrature of the Circle." In Famous Problems and Other Monographs. New York: Chelsea, pp. 16-23, 1980.
Krížek, M.; Luca, F.; and Somer, L. 17 Lectures on Fermat Numbers: From Number Theory to Geometry. New York: Springer-Verlag, 2001.
Sloane, N. J. A. Sequence A003401/M0505 in "The On-Line Encyclopedia of Integer Sequences."
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 137-138, 1990.
Wantzel, M. L. "Recherches sur les moyens de reconnaître si un problème de géométrie peut se résoudre avec la règle et le compas." J. Math. pures appliq. 1, 366-372, 1836.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















