


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-12-2020
Date: 14-11-2020
Date: 14-5-2020
|
The plastic constant 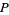 , sometimes also called the silver number or plastic number, is the limiting ratio of the successive terms of the Padovan sequence and Perrin sequence. It is given by
, sometimes also called the silver number or plastic number, is the limiting ratio of the successive terms of the Padovan sequence and Perrin sequence. It is given by
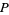 |
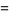 |
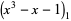 |
(1) |
 |
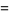 |
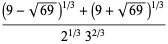 |
(2) |
 |
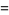 |
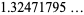 |
(3) |
(OEIS A060006), where 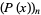 denotes a polynomial root. It is therefore an algebraic number of degree 3.
denotes a polynomial root. It is therefore an algebraic number of degree 3.
It is also given by
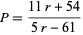 |
(4) |
where
![r=-1/5[-j(tau_0)]^(1/3),](http://mathworld.wolfram.com/images/equations/PlasticConstant/NumberedEquation2.gif) |
(5) |
where 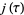 is the
is the 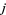 -function and the half-period ratio is equal to
-function and the half-period ratio is equal to 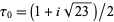 .
.
The plastic constant 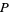 was originally studied in 1924 by Gérard Cordonnier when he was 17. In his later correspondence with Dom Hans van der Laan, he described applications to architecture, using the name "radiant number." In 1958, Cordonnier gave a lecture tour that illustrated the use of the constant in many existing buildings and monuments (C. Mannu, pers comm., Mar. 11, 2006).
was originally studied in 1924 by Gérard Cordonnier when he was 17. In his later correspondence with Dom Hans van der Laan, he described applications to architecture, using the name "radiant number." In 1958, Cordonnier gave a lecture tour that illustrated the use of the constant in many existing buildings and monuments (C. Mannu, pers comm., Mar. 11, 2006).
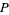 satisfies the algebraic identities
satisfies the algebraic identities
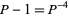 |
(6) |
and
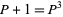 |
(7) |
and is therefore is one of the numbers  for which there exist natural numbers
for which there exist natural numbers 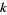 and
and 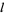 such that
such that 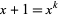 and
and 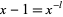 . It was proven by Aarts et al. (2001) that
. It was proven by Aarts et al. (2001) that 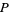 and the golden ratio
and the golden ratio 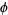 are in fact the only such numbers.
are in fact the only such numbers.
The identity 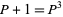 leads to the beautiful nested radical identity
leads to the beautiful nested radical identity
![P=RadicalBox[{1, +, RadicalBox[{1, +, RadicalBox[{1, +, ...}, 3]}, 3]}, 3].](http://mathworld.wolfram.com/images/equations/PlasticConstant/NumberedEquation5.gif) |
(8) |
The plastic constant is also connected with the ring of integers 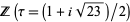 of the number field
of the number field 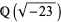 since it the real root of the Weber function for the smallest negative discriminant with class number 3, namely
since it the real root of the Weber function for the smallest negative discriminant with class number 3, namely 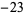 . In particular,
. In particular,
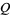 |
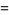 |
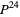 |
(9) |
 |
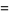 |
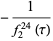 |
(10) |
 |
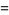 |
![-[(eta(tau))/(sqrt(2)eta(2tau))]^(24)](http://mathworld.wolfram.com/images/equations/PlasticConstant/Inline36.gif) |
(11) |
 |
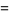 |
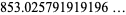 |
(12) |
(OEIS A116397), where 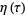 is the Dedekind eta function.
is the Dedekind eta function.
The plastic constant is also the smallest Pisot number.
The plastic constant satisfies the near-identity
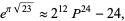 |
(13) |
where the difference is 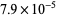 .
.
Surprisingly, the plastic constant is connected to the metric properties of the snub icosidodecadodecahedron.
REFERENCES:
Aarts, J.; Fokkink, R. J.; and Kruijtzer, G. "Morphic Numbers." Nieuw Arch. Wisk 5-2, 56-58, 2001. http://www.math.leidenuniv.nl/~naw/serie5/deel02/mrt2001/pdf/archi.pdf.
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 9, 2003.
Gazale, M. J. Ch. 7 in Gnomon: From Pharaohs to Fractals. Princeton, NJ: Princeton University Press, 1999.
Piezas, T. "Ramanujan's Constant and Its Cousins." http://www.geocities.com/titus_piezas/Ramanujan_a.htm.
Sloane, N. J. A. Sequences A060006 and A116397 in "The On-Line Encyclopedia of Integer Sequences."
Stewart, I. "Tales of a Neglected Number." Sci. Amer. 274, 102-103, Jun. 1996.
van der Laan, H. Le Nombre Plastique: quinze Leçons sur l'Ordonnance architectonique. Leiden: Brill, 1960.
Weng, A. "Class Polynomials of CM-Fields." http://www.exp-math.uni-essen.de/zahlentheorie/classpol/class.html.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|